Lösung 4.4:2e
Aus Online Mathematik Brückenkurs 1
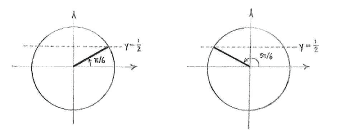
This is almost the same equation as in exercise d. First, we determine the solutions to the equation when \displaystyle 0\le \text{5}x\le \text{2}\pi , and using the unit circle shows that there are two of these: \displaystyle \text{5}x\text{ }=\frac{\pi }{6} and \displaystyle \text{5}x\text{ }=\pi -\frac{\pi }{6}=\frac{5\pi }{6}.
We obtain the remaining solutions by adding multiples of \displaystyle 2\pi to the two solutions above:
\displaystyle \text{5}x\text{ }=\frac{\pi }{6}+2n\pi
and
\displaystyle \text{5}x\text{ }=\frac{5\pi }{6}+2n\pi
(
\displaystyle n
an arbitrary integer),
or if we divide by \displaystyle \text{5}:
\displaystyle x\text{ }=\frac{\pi }{30}+\frac{2}{5}n\pi
and
\displaystyle x\text{ }=\frac{\pi }{6}+\frac{2}{5}n\pi
(
\displaystyle n
an arbitrary integer).