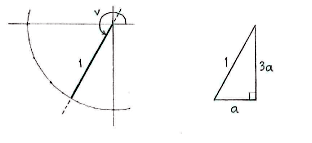Aus Online Mathematik Brückenkurs 1

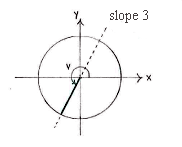
Because the angle \displaystyle v satisfies \displaystyle \pi \le v\le \frac{3\pi }{2}, \displaystyle v belongs to the third quadrant in the unit circle. Furthermore, \displaystyle \text{tan }v=\text{3 } gives that the line which corresponds to the angle \displaystyle v

\displaystyle v has a gradient of \displaystyle \text{3}.

slope 3

In the third quadrant, we can introduce a right-angled triangle in which the hypotenuse is \displaystyle \text{1} and the sides have a \displaystyle \text{3}:\text{1 } ratio.

If we now use Pythagoras' theorem on the triangle, we see that the horizontal side \displaystyle \text{a} satisfies

\displaystyle a^{2}+\left( 3a \right)^{2}=1^{2}

which gives us that

\displaystyle 10a^{2}=1 i.e. \displaystyle a=\frac{1}{\sqrt{10}}

Thus, the angle \displaystyle v's \displaystyle x -coordinate is \displaystyle -\frac{1}{\sqrt{10}} and \displaystyle y -coordinate is \displaystyle -\frac{3}{\sqrt{10}}, i.e.

\displaystyle \cos v=--\frac{1}{\sqrt{10}}

\displaystyle \sin v=-\frac{3}{\sqrt{10}}