Lösung 4.2:8

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
(Sprache und Formulierung)
Zeile 3: Zeile 3:
[[Image:4_2_8.gif|center]]
[[Image:4_2_8.gif|center]]
-
Durch die Definition von Kosinus können wir ''x'' und ''y'' berechnen
+
Durch die Definition von Kosinus können wir ''x'' und ''y'' berechnen:
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
-
x &= a\cos \alpha\,,\\[3pt]
+
x &= a\cos \alpha\,\text{ und}\\[3pt]
-
y &= b\cos \beta\,,
+
y &= b\cos \beta\,.
\end{align}</math>}}
\end{align}</math>}}
-
und für ''z'' erhalten wir analog
+
Für ''z'' erhalten wir analog
{{Abgesetzte Formel||<math>z=\ell\cos \gamma\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>z=\ell\cos \gamma\,\textrm{.}</math>}}
Zeile 22: Zeile 22:
{{Abgesetzte Formel||<math>\ell\cos \gamma = a\cos \alpha -b\cos \beta\,\textrm{,}</math>}}
{{Abgesetzte Formel||<math>\ell\cos \gamma = a\cos \alpha -b\cos \beta\,\textrm{,}</math>}}
-
wo <math>\gamma </math> der einziger unbekannter Variabel ist.
+
wobei <math>\gamma </math> hier die einzig verbleibende unbekannte Variable ist.

Version vom 13:32, 18. Jun. 2009

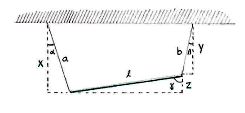
Wir zeichnen drei Dreiecke mit den vertikalen Seiten x, y und z, wie im Bild.

Durch die Definition von Kosinus können wir x und y berechnen:

\displaystyle \begin{align}

x &= a\cos \alpha\,\text{ und}\\[3pt] y &= b\cos \beta\,. \end{align}

Für z erhalten wir analog

\displaystyle z=\ell\cos \gamma\,\textrm{.}

Außerdem erfüllen die Längen x, y und z die Gleichung

\displaystyle z=x-y\,\textrm{.}

Ersetzen wir x, y und z mit unseren Ausdrücken oben, erhalten wir

\displaystyle \ell\cos \gamma = a\cos \alpha -b\cos \beta\,\textrm{,}

wobei \displaystyle \gamma hier die einzig verbleibende unbekannte Variable ist.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:8“