Lösung 4.2:5a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
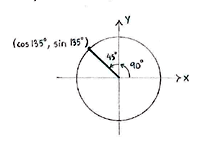
| - | Nachdem der Winkel <math>135^{\circ} = 90^{\circ} + 45^{\circ}</math>, <math>135^{\circ}</math> im zweiten | + | Nachdem der Winkel <math>135^{\circ} = 90^{\circ} + 45^{\circ}</math>, <math>135^{\circ}</math> im zweiten Quadranten liegt, bildet er den Winkel <math>45^{\circ}</math> mit der positiven ''y''-Achse |
[[Image:4_2_5_a1.gif|center]] | [[Image:4_2_5_a1.gif|center]] | ||
| - | Wir betrachten das Dreieck im zweiten Quadrant wie im Bild, um die Koordinaten des Punktes am Einheitskreis der den Winkel <math>135^{\circ}</math>entspricht zu bestimmen. | + | Wir betrachten das Dreieck im zweiten Quadrant wie im Bild, um die Koordinaten des Punktes am Einheitskreis, der den Winkel <math>135^{\circ}</math> entspricht, zu bestimmen. |
{| width="100%" | {| width="100%" | ||
| Zeile 10: | Zeile 10: | ||
|} | |} | ||
| - | Der Punkt hat also die Koordinaten <math>( -1/\!\sqrt{2}, 1/\!\sqrt{2})</math> | + | Der Punkt hat also die Koordinaten <math>( -1/\!\sqrt{2}, 1/\!\sqrt{2})</math>. Daher ist <math>\cos 135^{\circ} = -1/\!\sqrt{2}\,</math>. |
Version vom 13:24, 18. Jun. 2009
Nachdem der Winkel \displaystyle 135^{\circ} = 90^{\circ} + 45^{\circ}, \displaystyle 135^{\circ} im zweiten Quadranten liegt, bildet er den Winkel \displaystyle 45^{\circ} mit der positiven y-Achse
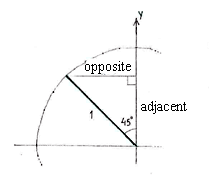
Wir betrachten das Dreieck im zweiten Quadrant wie im Bild, um die Koordinaten des Punktes am Einheitskreis, der den Winkel \displaystyle 135^{\circ} entspricht, zu bestimmen.
| \displaystyle \begin{align}\text{Gegenkathete} &= 1\cdot\sin 45^{\circ} = \dfrac{1}{\sqrt{2}}\\[5pt] \text{Ankathete} &= 1\cdot\cos 45^{\circ} = \frac{1}{\sqrt{2}}\end{align} |
Der Punkt hat also die Koordinaten \displaystyle ( -1/\!\sqrt{2}, 1/\!\sqrt{2}). Daher ist \displaystyle \cos 135^{\circ} = -1/\!\sqrt{2}\,.