Lösung 4.2:1c
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
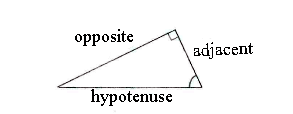
| - | Die Hypotenuse ist immer die Seite gegenüber des rechten Winkels, und auch immer die längste Seite des Dreiecks. Die Ankathete ist die Kathete am | + | Die Hypotenuse ist immer die Seite gegenüber des rechten Winkels, und auch immer die längste Seite des Dreiecks. Die Ankathete ist die Kathete am nächsten zum Winkel. |
[[Image:4_2_1_c.gif|center]] | [[Image:4_2_1_c.gif|center]] | ||
| - | Wir | + | Wir kennen die Länge der Gegenkathete und gefragt ist die Länge der Ankathete. Also betrachten wir den Tangens |
{{Abgesetzte Formel||<math>\tan 40^{\circ } = \frac{14}{x}</math>}} | {{Abgesetzte Formel||<math>\tan 40^{\circ } = \frac{14}{x}</math>}} | ||
Version vom 09:52, 18. Jun. 2009
Die Hypotenuse ist immer die Seite gegenüber des rechten Winkels, und auch immer die längste Seite des Dreiecks. Die Ankathete ist die Kathete am nächsten zum Winkel.
Wir kennen die Länge der Gegenkathete und gefragt ist die Länge der Ankathete. Also betrachten wir den Tangens
| \displaystyle \tan 40^{\circ } = \frac{14}{x} |
und erhalten
| \displaystyle x = \frac{14}{\tan 40^{\circ }}\quad \left( \approx 16\textrm{.}7 \right)\,\textrm{.} |