Lösung 2.3:8b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
Wir betrachten zuerst die Funktion <math>y=x^{2}+2</math>, wessen Graph eine Parabel ist, mit Minumum im Punkt (0,2). Der Graph der Funktion <math>y = (x-1)^{2}+2</math> ist wesentlich dieselbe Funktion, nus dass der ''x''-Wert immer um eine Einheit größer ist für denselben ''y''-Wert. Also ist die Parabel <math>y = (x-1)^{2}+2</math> die parabel <math>y=x^{2}+2</math> um eine Einheit nach rechts verschoben.
+
Wir betrachten zuerst die Funktion <math>y=x^{2}+2</math>, wessen Graph eine Parabel mit Minumum im Punkt (0,2) ist. Der Graph der Funktion <math>y = (x-1)^{2}+2</math> ist im Wesentlichen dieselbe Funktion, nur dass der ''x''-Wert immer um eine Einheit größer ist für denselben ''y''-Wert. Also ist die Parabel <math>y = (x-1)^{2}+2</math> die Parabel <math>y=x^{2}+2</math> um eine Einheit nach rechts verschoben.

Version vom 14:00, 9. Jun. 2009

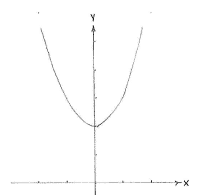
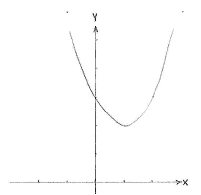
Wir betrachten zuerst die Funktion \displaystyle y=x^{2}+2, wessen Graph eine Parabel mit Minumum im Punkt (0,2) ist. Der Graph der Funktion \displaystyle y = (x-1)^{2}+2 ist im Wesentlichen dieselbe Funktion, nur dass der x-Wert immer um eine Einheit größer ist für denselben y-Wert. Also ist die Parabel \displaystyle y = (x-1)^{2}+2 die Parabel \displaystyle y=x^{2}+2 um eine Einheit nach rechts verschoben.


 
The graph of f(x) = x² + 2 The graph of f(x) = (x - 1)² + 2
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.3:8b“