Lösung 2.2:9b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
(Sprache und Formulierung)
Zeile 1: Zeile 1:
-
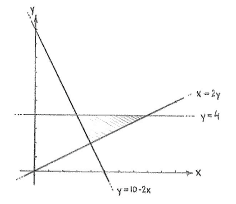
Zuerst zeichnen wir die Geraden, sodass wir sehen wie das Dreieck aussieht.
+
Zuerst zeichnen wir die Gerade, um zu sehen, wie das Dreieck aussieht.
[[Image:2_2_9_b-1(3).gif|center]]
[[Image:2_2_9_b-1(3).gif|center]]
-
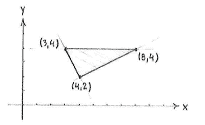
Die Ecken dieses Dreiecks, sind die Schnittpunkte des Geraden. Wir erhalten die Schnittstellen wenn wir die Gleichungen der Geraden für alle 3 Paare von geraden lösen.
+
Die Ecken dieses Dreiecks sind die Schnittpunkte der Geraden. Wir erhalten die Schnittstellen, wenn wir die Gleichungen der Geraden für alle 3 Paare von Geraden lösen.
{{Abgesetzte Formel||<math>\left\{\begin{align} x&=2y,\\ y&=4,\end{align}\right.\qquad
{{Abgesetzte Formel||<math>\left\{\begin{align} x&=2y,\\ y&=4,\end{align}\right.\qquad
\left\{\begin{align} x&=2y,\\ y&=10-2y,\end{align}\right.\qquad
\left\{\begin{align} x&=2y,\\ y&=10-2y,\end{align}\right.\qquad
-
\text{and}\qquad
+
\text{und}\qquad
\left\{\begin{align} y&=4,\\ y&=10-2y\,\textrm{.}\end{align}\right.</math>}}
\left\{\begin{align} y&=4,\\ y&=10-2y\,\textrm{.}\end{align}\right.</math>}}
Zeile 19: Zeile 19:
{{Abgesetzte Formel||<math>\text{Fläche} = \tfrac{1}{2}\cdot\text{(Basis)}\cdot\text{(Höhe),}</math>}}
{{Abgesetzte Formel||<math>\text{Fläche} = \tfrac{1}{2}\cdot\text{(Basis)}\cdot\text{(Höhe),}</math>}}
-
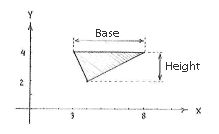
Nachdem hier eine Kante mit der ''x''-Achse parallel ist, wählen wir diese Kante als Basis des Dreiecks.
+
Nachdem hier eine Kante zur ''x''-Achse parallel ist, wählen wir diese Kante als Basis des Dreiecks.
Zeile 25: Zeile 25:
-
Die Basis ist einfach der Unterschied zwischen den ''x''-Koordinaten (3,4) und (8,4),
+
Die Basis ist Linie zwischen den ''x''-Koordinaten (3,4) und (8,4),
{{Abgesetzte Formel||<math>\text{Basis} = 8-3 = 5</math>}}
{{Abgesetzte Formel||<math>\text{Basis} = 8-3 = 5</math>}}
-
Wir erhalten die Höhe des Dreiecks als der Unterschied zwischen den ''x''-Koordinaten von dem Punkt (4,2) und von der Gerade <math>y=4</math>
+
Wir erhalten die Höhe des Dreiecks als Linie zwischen den ''x''-Koordinaten von dem Punkt (4,2) und von der Gerade <math>y=4</math>
{{Abgesetzte Formel||<math>\text{Höhe} = 4-2 = 2\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\text{Höhe} = 4-2 = 2\,\textrm{.}</math>}}
Zeile 35: Zeile 35:
Die Fläche des Dreiecks ist also
Die Fläche des Dreiecks ist also
-
{{Abgesetzte Formel||<math>\text{Fläche} = \tfrac{1}{2}\cdot\text{(Basis)}\cdot\text{(Höhe)} = \tfrac{1}{2}\cdot 5\cdot 2 = 5\,\text{u.a.}</math>}}
+
{{Abgesetzte Formel||<math>\text{Fläche} = \tfrac{1}{2}\cdot\text{(Basis)}\cdot\text{(Höhe)} = \tfrac{1}{2}\cdot 5\cdot 2 = 5\,\text{F.E.}</math>}}

Version vom 10:01, 9. Jun. 2009

Zuerst zeichnen wir die Gerade, um zu sehen, wie das Dreieck aussieht.

Die Ecken dieses Dreiecks sind die Schnittpunkte der Geraden. Wir erhalten die Schnittstellen, wenn wir die Gleichungen der Geraden für alle 3 Paare von Geraden lösen.

\displaystyle \left\{\begin{align} x&=2y,\\ y&=4,\end{align}\right.\qquad

\left\{\begin{align} x&=2y,\\ y&=10-2y,\end{align}\right.\qquad \text{und}\qquad \left\{\begin{align} y&=4,\\ y&=10-2y\,\textrm{.}\end{align}\right.

Die Gleichungssysteme haben die Lösungen \displaystyle (x,y) = (8,4), \displaystyle (x,y) = (4,2) und \displaystyle (x,y) = (3,4)\,.


Die Fläche des Dreiecks bekommen wir mit der Gleichung

\displaystyle \text{Fläche} = \tfrac{1}{2}\cdot\text{(Basis)}\cdot\text{(Höhe),}

Nachdem hier eine Kante zur x-Achse parallel ist, wählen wir diese Kante als Basis des Dreiecks.



Die Basis ist Linie zwischen den x-Koordinaten (3,4) und (8,4),

\displaystyle \text{Basis} = 8-3 = 5

Wir erhalten die Höhe des Dreiecks als Linie zwischen den x-Koordinaten von dem Punkt (4,2) und von der Gerade \displaystyle y=4

\displaystyle \text{Höhe} = 4-2 = 2\,\textrm{.}

Die Fläche des Dreiecks ist also

\displaystyle \text{Fläche} = \tfrac{1}{2}\cdot\text{(Basis)}\cdot\text{(Höhe)} = \tfrac{1}{2}\cdot 5\cdot 2 = 5\,\text{F.E.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:9b“