Lösung 4.4:4
Aus Online Mathematik Brückenkurs 1
K (hat „Solution 4.4:4“ nach „Lösung 4.4:4“ verschoben: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | Wir finden zuerst die allgemeine Lösung der Gleichung, und sehen danach welche der Winkeln im Intervall zwischen <math>0^{\circ}</math> und <math>360^{\circ}\,</math> liegen. | |
| - | + | Wir betrachten zuerst den Ausdruck <math>2v+10^{\circ}</math>, und erhalten die Lösung | |
{{Abgesetzte Formel||<math>2v + 10^{\circ} = 110^{\circ}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>2v + 10^{\circ} = 110^{\circ}\,\textrm{.}</math>}} | ||
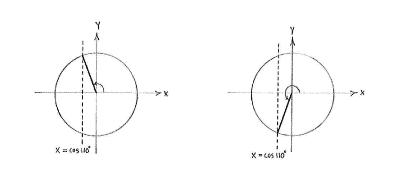
| + | Es gibt noch eine Lösung im Einheitskreis, nämlich im dritten Quadrant, mit denselben Winkel zur negativen ''y''-Achse, wie | ||
There is then a further solution which satisfies <math>0^{\circ}\le 2v + 10^{\circ}\le 360^{\circ}</math>, where <math>2v+10^{\circ}</math> lies in the third quadrant and makes the same angle with the negative ''y''-axis as <math>100^{\circ}</math> makes with the positive ''y''-axis, i.e. <math>2v + 10^{\circ}</math> makes an angle <math>110^{\circ} - 90^{\circ} = 20^{\circ}</math> | There is then a further solution which satisfies <math>0^{\circ}\le 2v + 10^{\circ}\le 360^{\circ}</math>, where <math>2v+10^{\circ}</math> lies in the third quadrant and makes the same angle with the negative ''y''-axis as <math>100^{\circ}</math> makes with the positive ''y''-axis, i.e. <math>2v + 10^{\circ}</math> makes an angle <math>110^{\circ} - 90^{\circ} = 20^{\circ}</math> | ||
with the negative ''y''-axis and consequently | with the negative ''y''-axis and consequently | ||
Version vom 09:30, 7. Apr. 2009
Wir finden zuerst die allgemeine Lösung der Gleichung, und sehen danach welche der Winkeln im Intervall zwischen \displaystyle 0^{\circ} und \displaystyle 360^{\circ}\, liegen.
Wir betrachten zuerst den Ausdruck \displaystyle 2v+10^{\circ}, und erhalten die Lösung
| \displaystyle 2v + 10^{\circ} = 110^{\circ}\,\textrm{.} |
Es gibt noch eine Lösung im Einheitskreis, nämlich im dritten Quadrant, mit denselben Winkel zur negativen y-Achse, wie There is then a further solution which satisfies \displaystyle 0^{\circ}\le 2v + 10^{\circ}\le 360^{\circ}, where \displaystyle 2v+10^{\circ} lies in the third quadrant and makes the same angle with the negative y-axis as \displaystyle 100^{\circ} makes with the positive y-axis, i.e. \displaystyle 2v + 10^{\circ} makes an angle \displaystyle 110^{\circ} - 90^{\circ} = 20^{\circ} with the negative y-axis and consequently
| \displaystyle 2v + 10^{\circ} = 270^{\circ} - 20^{\circ} = 250^{\circ}\,\textrm{.} |
Now it is easy to write down the general solution,
| \displaystyle \left\{\begin{align} 2v + 10^{\circ} &= 110^{\circ} + n\cdot 360^{\circ}\quad\text{and}\\[5pt] 2v + 10^{\circ} &= 250^{\circ} + n\cdot 360^{\circ}\,,\end{align}\right. |
and if we make v the subject, we get
| \displaystyle \left\{\begin{align} v &= 50^{\circ} + n\cdot 180^{\circ}\quad\text{and}\\[5pt] v &= 120^{\circ} + n\cdot 180^{\circ}\end{align}\right. |
For different values of the integers n, we see that the corresponding solutions are:
| \displaystyle \cdots\cdots | \displaystyle \cdots\cdots | \displaystyle \cdots\cdots | ||
| \displaystyle n=-2: | \displaystyle v = 50^{\circ} - 2\cdot 180^{\circ} = -310^{\circ} | \displaystyle v = 120^{\circ } - 2\cdot 180^{\circ} = -240^{\circ} | ||
| \displaystyle n=-1: | \displaystyle v = 50^{\circ} - 1\cdot 180^{\circ} = -130^{\circ} | \displaystyle v = 120^{\circ} - 1\cdot 180^{\circ} = -60^{\circ} | ||
| \displaystyle n=0: | \displaystyle v = 50^{\circ} + 0\cdot 180^{\circ} = 50^{\circ} | \displaystyle v = 120^{\circ} + 0\cdot 180^{\circ} = 120^{\circ} | ||
| \displaystyle n=1: | \displaystyle v = 50^{\circ} + 1\cdot 180^{\circ} = 230^{\circ} | \displaystyle v = 120^{\circ} + 1\cdot 180^{\circ} = 300^{\circ} | ||
| \displaystyle n=2: | \displaystyle v = 50^{\circ} + 2\cdot 180^{\circ} = 410^{\circ} | \displaystyle v = 120^{\circ} + 2\cdot 180^{\circ} = 480^{\circ} | ||
| \displaystyle n=3: | \displaystyle v = 50^{\circ} + 3\cdot 180^{\circ} = 590^{\circ} | \displaystyle v = 120^{\circ} + 3\cdot 180^{\circ} = 660^{\circ} | ||
| \displaystyle \cdots\cdots | \displaystyle \cdots\cdots | \displaystyle \cdots\cdots |
From the table, we see that the solutions that are between \displaystyle 0^{\circ} and \displaystyle 360^{\circ} are
| \displaystyle v = 50^{\circ},\quad v=120^{\circ },\quad v=230^{\circ}\quad\text{and}\quad v=300^{\circ}\,\textrm{.} |