Lösung 4.4:2f

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.4:2f“ nach „Lösung 4.4:2f“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
Using the unit circle shows that the equation <math>\cos 3x = -1/\!\sqrt{2}</math>
+
Durch den Einheitskreis sehen wir dass die Gleichung <math>\cos 3x = -1/\!\sqrt{2}</math> zwei Lösungen im Intervall <math>0\le 3x\le 2\pi\,</math> hat,
-
has two solutions for <math>0\le 3x\le 2\pi\,</math>,
+
-
{{Abgesetzte Formel||<math>3x = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\qquad\text{and}\qquad 3x = \pi + \frac{\pi}{4} = \frac{5\pi}{4}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>3x = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\qquad\text{und}\qquad 3x = \pi + \frac{\pi}{4} = \frac{5\pi}{4}\,\textrm{.}</math>}}
[[Image:4_4_2_f.gif|center]]
[[Image:4_4_2_f.gif|center]]
-
We obtain the other solutions by adding multiples of <math>2\pi</math>,
+
Wir addieren einen Multipel von <math>2\pi</math> um die allgemeine Lösung zu erhalten,
-
{{Abgesetzte Formel||<math>3x = \frac{3\pi}{4} + 2n\pi\qquad\text{and}\qquad 3x = \frac{5\pi}{4} + 2n\pi\,,</math>}}
+
{{Abgesetzte Formel||<math>3x = \frac{3\pi}{4} + 2n\pi\qquad\text{und}\qquad 3x = \frac{5\pi}{4} + 2n\pi\,,</math>}}
-
i.e.
+
oder, nach Division durch 3,
-
{{Abgesetzte Formel||<math>x = \frac{\pi}{4} + \frac{2}{3}n\pi\qquad\text{and}\qquad x = \frac{5\pi}{12} + \frac{2}{3}n\pi\,,</math>}}
+
{{Abgesetzte Formel||<math>x = \frac{\pi}{4} + \frac{2}{3}n\pi\qquad\text{und}\qquad x = \frac{5\pi}{12} + \frac{2}{3}n\pi\,,</math>}}
-
 
+
-
where ''n'' is an arbitrary integer.
+

Version vom 21:17, 5. Apr. 2009

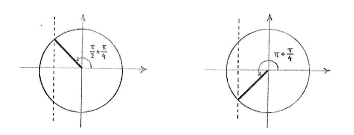
Durch den Einheitskreis sehen wir dass die Gleichung \displaystyle \cos 3x = -1/\!\sqrt{2} zwei Lösungen im Intervall \displaystyle 0\le 3x\le 2\pi\, hat,

\displaystyle 3x = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\qquad\text{und}\qquad 3x = \pi + \frac{\pi}{4} = \frac{5\pi}{4}\,\textrm{.}

Wir addieren einen Multipel von \displaystyle 2\pi um die allgemeine Lösung zu erhalten,

\displaystyle 3x = \frac{3\pi}{4} + 2n\pi\qquad\text{und}\qquad 3x = \frac{5\pi}{4} + 2n\pi\,,

oder, nach Division durch 3,

\displaystyle x = \frac{\pi}{4} + \frac{2}{3}n\pi\qquad\text{und}\qquad x = \frac{5\pi}{12} + \frac{2}{3}n\pi\,,
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:2f“