Lösung 4.4:1g

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.4:1g“ nach „Lösung 4.4:1g“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
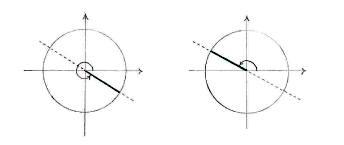
A quick sketch of the unit circle and the line <math>y=(-1/\!\sqrt{3})x</math>, which corresponds to the tangent value <math>-1/\!\sqrt{3}</math> shows that there are two angles which satisfy <math>\tan v = -1/\!\sqrt{3}</math>. One of the angles lies in the fourth quadrant and the other is the opposite angle in the second quadrant.
+
Zeichnen wir den Einheitskreis mit der Geraden <math>y=(-1/\!\sqrt{3})x</math>, was also den Winkel mit den Tangens <math>-1/\!\sqrt{3}</math> entspricht, sehen wir dass es zwei Winkeln gibt die die Gleichung <math>\tan v = -1/\!\sqrt{3}</math> erfüllen. Diese liegen gegenüber von einander im zweiten und im vierten Quadrant.
[[Image:4_4_1_g1.gif|center]]
[[Image:4_4_1_g1.gif|center]]
-
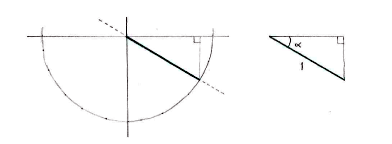
We can therefore limit ourselves to the fourth quadrant and draw an auxiliary triangle in order to determine the angle there.
+
Wir betrachten nur den vierten Quadrant, und führen ein neues Dreieck ein, siehe Bild.
[[Image:4_4_1_g2.gif|center]]
[[Image:4_4_1_g2.gif|center]]
-
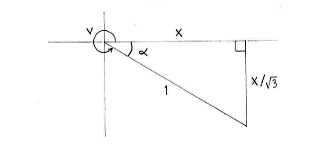
If we call <math>x</math> the side adjacent to the angle <math>\alpha</math> then the fact that <math>\tan v=-1/\!\sqrt{3}</math> gives the length of the opposite side as <math>x/\!\sqrt{3}</math>.
+
Wir benennen die Ankathete <math>x</math> und nachdem <math>\tan v=-1/\!\sqrt{3}</math> ist die Länge der Gegenkathete <math>x/\!\sqrt{3}</math>.
[[Image:4_4_1_g3.gif|center]]
[[Image:4_4_1_g3.gif|center]]
-
The Pythagorean theorem gives
+
Durch das Gesetz des Pythagoras erhalten wir
{{Abgesetzte Formel||<math>x^2 + \Bigl(\frac{x}{\sqrt{3}}\Bigr)^2 = 1^2</math>}}
{{Abgesetzte Formel||<math>x^2 + \Bigl(\frac{x}{\sqrt{3}}\Bigr)^2 = 1^2</math>}}
-
and this equation has the solution <math>x = \sqrt{3}/2</math>, which means that
+
Diese Gleichung hat die positive Lösung <math>x = \sqrt{3}/2</math>, und also haben wir
{{Abgesetzte Formel||<math>\cos\alpha = \frac{\sqrt{3}/2}{1} = \frac{\sqrt{3}}{2}\,,</math>}}
{{Abgesetzte Formel||<math>\cos\alpha = \frac{\sqrt{3}/2}{1} = \frac{\sqrt{3}}{2}\,,</math>}}
-
i.e. <math>\alpha = \pi/6</math>. Because the angle <math>v</math> in the fourth quadrant is the complement of <math>\alpha</math> the angle <math>v</math> is given by
+
also ist <math>\alpha = \pi/6</math>. Nachdem der Winkel <math>v</math> das Komplement des Winkels <math>\alpha</math> ist, ist <math>v</math>
{{Abgesetzte Formel||<math>v = 2\pi - \alpha = 2\pi - \frac{\pi}{6} = \frac{11\pi }{6}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>v = 2\pi - \alpha = 2\pi - \frac{\pi}{6} = \frac{11\pi }{6}\,\textrm{.}</math>}}
-
If we subtract half a turn, <math>\pi</math>, we obtain the other angle
+
Subtrahieren wir <math>\pi</math> von <math>v</math> erhalten wir den anderen Winkel in zweiten Quadrant,
{{Abgesetzte Formel||<math>v = \frac{11\pi}{6} - \pi = \frac{5\pi}{6}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>v = \frac{11\pi}{6} - \pi = \frac{5\pi}{6}\,\textrm{.}</math>}}

Version vom 20:47, 5. Apr. 2009

Zeichnen wir den Einheitskreis mit der Geraden \displaystyle y=(-1/\!\sqrt{3})x, was also den Winkel mit den Tangens \displaystyle -1/\!\sqrt{3} entspricht, sehen wir dass es zwei Winkeln gibt die die Gleichung \displaystyle \tan v = -1/\!\sqrt{3} erfüllen. Diese liegen gegenüber von einander im zweiten und im vierten Quadrant.

Wir betrachten nur den vierten Quadrant, und führen ein neues Dreieck ein, siehe Bild.

Wir benennen die Ankathete \displaystyle x und nachdem \displaystyle \tan v=-1/\!\sqrt{3} ist die Länge der Gegenkathete \displaystyle x/\!\sqrt{3}.

Durch das Gesetz des Pythagoras erhalten wir

\displaystyle x^2 + \Bigl(\frac{x}{\sqrt{3}}\Bigr)^2 = 1^2

Diese Gleichung hat die positive Lösung \displaystyle x = \sqrt{3}/2, und also haben wir

\displaystyle \cos\alpha = \frac{\sqrt{3}/2}{1} = \frac{\sqrt{3}}{2}\,,

also ist \displaystyle \alpha = \pi/6. Nachdem der Winkel \displaystyle v das Komplement des Winkels \displaystyle \alpha ist, ist \displaystyle v

\displaystyle v = 2\pi - \alpha = 2\pi - \frac{\pi}{6} = \frac{11\pi }{6}\,\textrm{.}

Subtrahieren wir \displaystyle \pi von \displaystyle v erhalten wir den anderen Winkel in zweiten Quadrant,

\displaystyle v = \frac{11\pi}{6} - \pi = \frac{5\pi}{6}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:1g“