Lösung 4.4:1b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.4:1b“ nach „Lösung 4.4:1b“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
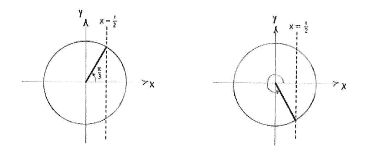
The easiest angle to find is <math>v = \pi/3</math> in the first quadrant. When we draw the unit circle, we see that the angle which makes the same angle with the positive ''x''-axis as <math>v=\pi/3</math>, but is under the ''x''-axis, also has a cosine value of 1/2 (same ''x''-coordinate).
+
Wir wissen von vorher dass <math>v = \pi/3</math> im ersten Quadrant eine Lösung ist. Zeichnen wir den Einheitskreis sehen wir dass, auf Grund der Symmetrie, der negative Winkel <math>v=\pi/3</math> dieselbe ''x''-Koordinate hat.
[[Image:4_4_1_b.gif|center]]
[[Image:4_4_1_b.gif|center]]
-
There are thus two angles, <math>v=\pi/3</math> and <math>v=2\pi - \pi/3 = 5\pi/3</math> which have their cosine value equal to 1/2.
+
Also gibt es zwei Winkeln, <math>v=\pi/3</math> und <math>v=2\pi - \pi/3 = 5\pi/3</math> deren Kosinus 1/2 ist.

Version vom 20:23, 5. Apr. 2009

Wir wissen von vorher dass \displaystyle v = \pi/3 im ersten Quadrant eine Lösung ist. Zeichnen wir den Einheitskreis sehen wir dass, auf Grund der Symmetrie, der negative Winkel \displaystyle v=\pi/3 dieselbe x-Koordinate hat.

Also gibt es zwei Winkeln, \displaystyle v=\pi/3 und \displaystyle v=2\pi - \pi/3 = 5\pi/3 deren Kosinus 1/2 ist.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:1b“