Lösung 4.3:3d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (hat „Solution 4.3:3d“ nach „Lösung 4.3:3d“ verschoben: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | Der Winkel <math>\pi/2 - v</math> hat denselben Winkel zur positiven ''y''-Achse, wie der Winkel <math>-v</math> zur positiven ''x''-Achse hat. | |
{| align="center" | {| align="center" | ||
| Zeile 11: | Zeile 11: | ||
|} | |} | ||
| - | + | Also hat der Winkel <math>\pi/2 - v</math> dieselbe ''y''-Koordinate, wie die ''x''-Koordinate de Winkels math>v</math>. | |
{{Abgesetzte Formel||<math>\sin\Bigl(\frac{\pi}{2} - v\Bigr) = \cos v</math>}} | {{Abgesetzte Formel||<math>\sin\Bigl(\frac{\pi}{2} - v\Bigr) = \cos v</math>}} | ||
| - | + | Und von der Übung c wissen wir dass <math>\cos v = \sqrt{1-a^2}\,</math>, also haben wir | |
{{Abgesetzte Formel||<math>\sin\Bigl(\frac{\pi}{2}-v\Bigr) = \sqrt{1-a^2}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>\sin\Bigl(\frac{\pi}{2}-v\Bigr) = \sqrt{1-a^2}\,\textrm{.}</math>}} | ||
Version vom 12:16, 5. Apr. 2009
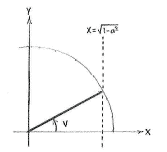
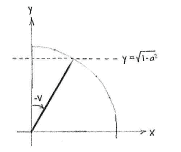
Der Winkel \displaystyle \pi/2 - v hat denselben Winkel zur positiven y-Achse, wie der Winkel \displaystyle -v zur positiven x-Achse hat.
| 
| |
| Angle v | Angle π/2 - v |
Also hat der Winkel \displaystyle \pi/2 - v dieselbe y-Koordinate, wie die x-Koordinate de Winkels math>v</math>.
| \displaystyle \sin\Bigl(\frac{\pi}{2} - v\Bigr) = \cos v |
Und von der Übung c wissen wir dass \displaystyle \cos v = \sqrt{1-a^2}\,, also haben wir
| \displaystyle \sin\Bigl(\frac{\pi}{2}-v\Bigr) = \sqrt{1-a^2}\,\textrm{.} |
