Lösung 4.2:4b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (hat „Solution 4.2:4b“ nach „Lösung 4.2:4b“ verschoben: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | Zuerst subtrahieren wir <math>2\pi</math> von <math>11\pi/3</math>, sodass wir einen Winkel zwischen <math>0</math> und <math>2\pi </math> erhalten. Dies ändert nicht den Wert des Kosinus. | |
{{Abgesetzte Formel||<math>\cos\frac{11\pi}{3} = \cos\Bigl(\frac{11\pi}{3}-2\pi\Bigr) = \cos\frac{5\pi}{3}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>\cos\frac{11\pi}{3} = \cos\Bigl(\frac{11\pi}{3}-2\pi\Bigr) = \cos\frac{5\pi}{3}\,\textrm{.}</math>}} | ||
| - | + | Danach schreiben wir <math>5\pi/3</math> wie eine Summe von <math>\pi</math>- und <math>\pi/2</math>-Termen, | |
{{Abgesetzte Formel||<math>\frac{5\pi}{3} = \frac{3\pi +\dfrac{3}{2}\pi +\dfrac{1}{2}\pi}{3} = \pi + \frac{\pi}{2} + \frac{\pi}{6}</math>}} | {{Abgesetzte Formel||<math>\frac{5\pi}{3} = \frac{3\pi +\dfrac{3}{2}\pi +\dfrac{1}{2}\pi}{3} = \pi + \frac{\pi}{2} + \frac{\pi}{6}</math>}} | ||
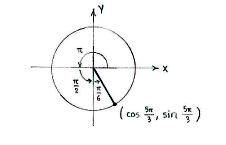
| - | + | So sehen wir dass <math>5\pi/3</math> im vierten Quadrant liegt, und den Winkel <math>\pi/6</math> mit der negativen ''y''-Achse bildet. | |
[[Image:4_2_4b1.gif||center]] | [[Image:4_2_4b1.gif||center]] | ||
| - | + | Mit ein Wenig Trigonometrie berechnen wir den Punkt am Einheitskreis, der den Winkel <math>5\pi/3\,</math> entspricht, | |
| - | <math>5\pi/3\,</math> | + | |
{| width="100%" | {| width="100%" | ||
|width="50%" align="center"|[[Image:4_2_4_b2.gif]] | |width="50%" align="center"|[[Image:4_2_4_b2.gif]] | ||
| - | |width="50%" align="left"|<math>\begin{align}\text{ | + | |width="50%" align="left"|<math>\begin{align}\text{Gegenkathete} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{Ankathete} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align}</math> |
|} | |} | ||
| - | + | Der Punkt hat also die Koordinaten <math>(1/2,-\sqrt{3}/2)</math> und | |
{{Abgesetzte Formel||<math>\cos \frac{11\pi}{3} = \cos\frac{5\pi}{3} = \frac{1}{2}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>\cos \frac{11\pi}{3} = \cos\frac{5\pi}{3} = \frac{1}{2}\,\textrm{.}</math>}} | ||
Version vom 15:03, 4. Apr. 2009
Zuerst subtrahieren wir \displaystyle 2\pi von \displaystyle 11\pi/3, sodass wir einen Winkel zwischen \displaystyle 0 und \displaystyle 2\pi erhalten. Dies ändert nicht den Wert des Kosinus.
| \displaystyle \cos\frac{11\pi}{3} = \cos\Bigl(\frac{11\pi}{3}-2\pi\Bigr) = \cos\frac{5\pi}{3}\,\textrm{.} |
Danach schreiben wir \displaystyle 5\pi/3 wie eine Summe von \displaystyle \pi- und \displaystyle \pi/2-Termen,
| \displaystyle \frac{5\pi}{3} = \frac{3\pi +\dfrac{3}{2}\pi +\dfrac{1}{2}\pi}{3} = \pi + \frac{\pi}{2} + \frac{\pi}{6} |
So sehen wir dass \displaystyle 5\pi/3 im vierten Quadrant liegt, und den Winkel \displaystyle \pi/6 mit der negativen y-Achse bildet.
Mit ein Wenig Trigonometrie berechnen wir den Punkt am Einheitskreis, der den Winkel \displaystyle 5\pi/3\, entspricht,
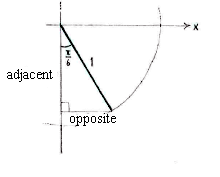
| \displaystyle \begin{align}\text{Gegenkathete} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{Ankathete} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align} |
Der Punkt hat also die Koordinaten \displaystyle (1/2,-\sqrt{3}/2) und
| \displaystyle \cos \frac{11\pi}{3} = \cos\frac{5\pi}{3} = \frac{1}{2}\,\textrm{.} |