Lösung 4.2:3e

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.2:3e“ nach „Lösung 4.2:3e“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
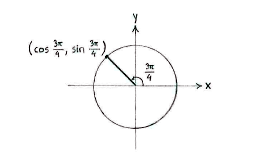
If we draw the line which has angle <math>3\pi/4</math> relative to the positive ''x''-axis, it will cut the unit circle in the second quadrant.
+
Die Gerade mit dem Winkel <math>3\pi/4</math> zur positiven ''x''-Achse wird den Einheitskreis im zweiten Quadrant schneiden.
[[Image:4_2_3_e1.gif|center]]
[[Image:4_2_3_e1.gif|center]]
-
At first sight, the figure gives information about the signs of <math>\cos (3\pi/4)</math> and <math>\sin (3\pi/4)</math>: cosine, which is the ''x''-coordinate for the intersection point, is negative, whereas sine, which is the ''y''-coordinate for the intersection point, is positive.
+
Nachdem die 'y''-Koordinate vom Schnittpunkt positiv ist, ist auch <math>\sin (3\pi/4)</math> positiv.
-
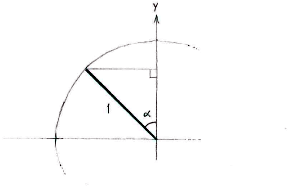
In order to go further and determine the coordinates of the intersection points, we concentrate on the second quadrant and introduce an auxiliary triangle which has the line associated with the angle as the hypotenuse and its other edges parallel to the coordinate axes.
+
Wir betrachten das Dreieck im zweiten Quadrant, dass die Gerade mit den Winkel <math>\sin (3\pi/4)</math> zur ''x''-Achse als Hypotenuse hat, und wo die Katheten parallel mit den Koordinatenachsen sind.
[[Image:4_2_3_e_2.gif|center]]
[[Image:4_2_3_e_2.gif|center]]
-
In this triangle, we see that the angle <math>\alpha</math> between the hypotenuse and the ''y''-axis is the part of the angle <math>3\pi/4</math> that lies in the second quadrant, i.e. <math>\alpha = 3\pi/4 - \pi/2 = \pi/4\,</math>. With the help of trigonometry, we can now determine the triangle's sides.
+
In diesen Dreieck sehen wir dass der Winkel <math>\alpha</math> zwischen der Hypotenuse und der ''y''-Achse, der teil des Winkels <math>3\pi/4</math> der in den zweiten Quadrant liegt. Also ist <math>\alpha = 3\pi/4 - \pi/2 = \pi/4\,</math>. Wir können die Seiten des Dreiecks mit Trigonometrie berechnen.
{| width="100%"
{| width="100%"
Zeile 16: Zeile 16:
|}
|}
-
This shows that the intersection point has coordinates
+
Also hat die Schnittstelle zwischen der geraden und den Einheitskreis die Koordinaten
-
<math>(-1/\!\sqrt{2}, 1/\!\sqrt{2})</math> (note the minus sign in the ''x''-coordinate) and therefore that <math>\sin (3\pi/4) = 1/\!\sqrt{2}\,</math>.
+
<math>(-1/\!\sqrt{2}, 1/\!\sqrt{2})</math> und also ist <math>\sin (3\pi/4) = 1/\!\sqrt{2}\,</math>.

Version vom 12:55, 4. Apr. 2009

Die Gerade mit dem Winkel \displaystyle 3\pi/4 zur positiven x-Achse wird den Einheitskreis im zweiten Quadrant schneiden.

Nachdem die 'y-Koordinate vom Schnittpunkt positiv ist, ist auch \displaystyle \sin (3\pi/4) positiv.

Wir betrachten das Dreieck im zweiten Quadrant, dass die Gerade mit den Winkel \displaystyle \sin (3\pi/4) zur x-Achse als Hypotenuse hat, und wo die Katheten parallel mit den Koordinatenachsen sind.

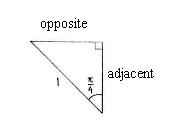
In diesen Dreieck sehen wir dass der Winkel \displaystyle \alpha zwischen der Hypotenuse und der y-Achse, der teil des Winkels \displaystyle 3\pi/4 der in den zweiten Quadrant liegt. Also ist \displaystyle \alpha = 3\pi/4 - \pi/2 = \pi/4\,. Wir können die Seiten des Dreiecks mit Trigonometrie berechnen.

\displaystyle \begin{align}\text{opposite} &= 1\cdot\sin\frac{\pi}{4} = \frac{1}{\sqrt{2}}\\[5pt] \text{adjacent} &= 1\cdot\cos\frac{\pi}{4} = \frac{1}{\sqrt{2}}\end{align}

Also hat die Schnittstelle zwischen der geraden und den Einheitskreis die Koordinaten \displaystyle (-1/\!\sqrt{2}, 1/\!\sqrt{2}) und also ist \displaystyle \sin (3\pi/4) = 1/\!\sqrt{2}\,.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:3e“