Lösung 4.2:2a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.2:2a“ nach „Lösung 4.2:2a“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
The opposite and adjacent are given in the right-angled triangle and this means that the value of the tangent for the angle can be determined as the quotient between the opposite and the adjacent:
+
Wir wissen die Längen der Katheten im Dreieck, und also können wir den Tangens für den Winkel ''w'' in den Katheten ausdrücken,
{| width="100%"
{| width="100%"
Zeile 6: Zeile 6:
|}
|}
-
At the same time, this is a trigonometric equation for the angle ''v''.
+
Dies ist eine Trigonometrische Gleichung die ''v'' erfüllt.
-
 
+
-
 
+
-
Note: In the chapter on "Trigonometric equations", we will investigate more closely how to solve equations of this type.
+

Version vom 12:02, 4. Apr. 2009

Wir wissen die Längen der Katheten im Dreieck, und also können wir den Tangens für den Winkel w in den Katheten ausdrücken,

\displaystyle \tan v = 2/5 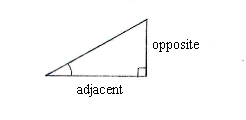Image:4_2_2_a.gif

Dies ist eine Trigonometrische Gleichung die v erfüllt.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:2a“