Lösung 4.2:1f
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (hat „Solution 4.2:1f“ nach „Lösung 4.2:1f“ verschoben: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
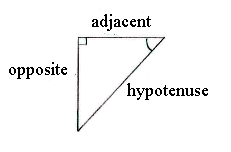
| - | + | Die Ankathete zum Winkel 50° ist ''x'', und die Gegenkathete hat die Länge 19. | |
[[Image:4_2_1_f.gif|center]] | [[Image:4_2_1_f.gif|center]] | ||
| - | + | Wir betrachten den Ausdruck für Tangens und erhalten | |
{{Abgesetzte Formel||<math>\tan 50^{\circ} = \frac{19}{x}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>\tan 50^{\circ} = \frac{19}{x}\,\textrm{.}</math>}} | ||
| - | + | und also | |
{{Abgesetzte Formel||<math>x=\frac{19}{\tan 50^{\circ }}\quad ({}\approx 15\textrm{.}9)\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>x=\frac{19}{\tan 50^{\circ }}\quad ({}\approx 15\textrm{.}9)\,\textrm{.}</math>}} | ||
Version vom 11:55, 4. Apr. 2009
Die Ankathete zum Winkel 50° ist x, und die Gegenkathete hat die Länge 19.
Wir betrachten den Ausdruck für Tangens und erhalten
| \displaystyle \tan 50^{\circ} = \frac{19}{x}\,\textrm{.} |
und also
| \displaystyle x=\frac{19}{\tan 50^{\circ }}\quad ({}\approx 15\textrm{.}9)\,\textrm{.} |