Lösung 4.2:1a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.2:1a“ nach „Lösung 4.2:1a“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
The definition of the tangent states that
+
Die Definition von Tangens ist
{| width="100%"
{| width="100%"
-
| width="50%" align="center"|<math>\tan u=\frac{\text{opposite}}{\text{adjacent}}</math>
+
| width="50%" align="center"|<math>\tan u=\frac{\text{Gegenkathete}}{\text{Ankathete}}</math>
| width="50%" align="center"|[[Image:4_2_1_a.gif]]
| width="50%" align="center"|[[Image:4_2_1_a.gif]]
|}
|}
-
In our case, this means that
+
In unseren Fall haben wir
{{Abgesetzte Formel||<math>\tan 27^{\circ} = \frac{x}{13}</math>}}
{{Abgesetzte Formel||<math>\tan 27^{\circ} = \frac{x}{13}</math>}}
-
which gives <math>x = 13\cdot \tan 27^{\circ}\,</math>.
+
und also ist <math>x = 13\cdot \tan 27^{\circ}\,</math>.
-
 
+
Hinweis: mit einem Taschenrechner können wir ''x'' bestimmen;
-
Note: Using a calculator, we can work out what ''x'' should be,
+
{{Abgesetzte Formel||<math>x = 13\cdot\tan 27^{\circ} \approx 6\textrm{.}62\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>x = 13\cdot\tan 27^{\circ} \approx 6\textrm{.}62\,\textrm{.}</math>}}

Version vom 11:44, 4. Apr. 2009

Die Definition von Tangens ist

\displaystyle \tan u=\frac{\text{Gegenkathete}}{\text{Ankathete}} 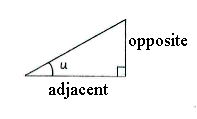Image:4_2_1_a.gif

In unseren Fall haben wir

\displaystyle \tan 27^{\circ} = \frac{x}{13}

und also ist \displaystyle x = 13\cdot \tan 27^{\circ}\,.

Hinweis: mit einem Taschenrechner können wir x bestimmen;

\displaystyle x = 13\cdot\tan 27^{\circ} \approx 6\textrm{.}62\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:1a“