4.1 Winkel und Kreise
Aus Online Mathematik Brückenkurs 1
K (Robot: Automated text replacement (-Useful([\s\n]+)web([\s\n]+)sites +Nützliche Websites)) |
|||
| Zeile 18: | Zeile 18: | ||
'''Lernziele:''' | '''Lernziele:''' | ||
| - | Nach diesem Abschnitt | + | Nach diesem Abschnitt sollten Sie folgendes können : |
*To convert between degrees, radians and revolutions. | *To convert between degrees, radians and revolutions. | ||
*To calculate the area and circumference of sectors of a circle. | *To calculate the area and circumference of sectors of a circle. | ||
| Zeile 29: | Zeile 29: | ||
}} | }} | ||
| - | == | + | == Winkeleinheiten == |
| - | + | Es gibt viele verschiedene Winkeleinheiten, die in verschiedenen Gebieten verwendet werden. Die zwei häufigsten sind Grad und Radiant. | |
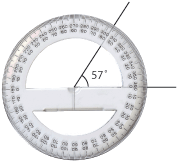
| - | *''' | + | *'''Grad.''' Wenn man einen Kreis in 360 gleich große Stücke aufteilt, hat ein Stück den Winkel. Man bezeichnet die Einheit Grad mit <math>{}^\circ</math>. |
[[Image:Gradskiva - 57°.gif||center]] | [[Image:Gradskiva - 57°.gif||center]] | ||
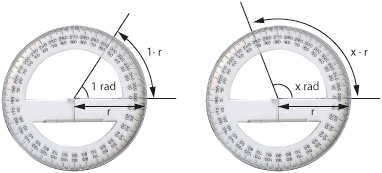
| - | *''' | + | *'''Radiant.''' Eine andere Winkeleinheit ist der Radiant. Der Radiant wird oft ''rad'' geschrieben. Ein Radiant wird definiert dadurch dass ein Kreis den Winkel <math>2\pi</math> rad hat. |
[[Image:Gradskiva - Radianer.gif||center]] | [[Image:Gradskiva - Radianer.gif||center]] | ||
| - | + | Ein Vollreis besteht aus <math>360^\circ</math> oder <math>2\pi</math> rad, und also ist | |
{{Abgesetzte Formel||<math>\begin{align*} | {{Abgesetzte Formel||<math>\begin{align*} | ||
&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians } | &1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians } | ||
| Zeile 49: | Zeile 49: | ||
= \frac{180^\circ}{\pi}\,\mbox{.} | = \frac{180^\circ}{\pi}\,\mbox{.} | ||
\end{align*}</math>}} | \end{align*}</math>}} | ||
| - | + | Mit diesen Verhältnis kann man Winkeln zwischen den Einheiten Grad und Radiant umwandeln. | |
<div class="exempel"> | <div class="exempel"> | ||
| Zeile 56: | Zeile 56: | ||
<ol type="a"> | <ol type="a"> | ||
<li><math>30^\circ = 30 \cdot 1^\circ | <li><math>30^\circ = 30 \cdot 1^\circ | ||
| - | = 30 \cdot \frac{\pi}{180}\ \mbox{ | + | = 30 \cdot \frac{\pi}{180}\ \mbox{ rad } |
| - | = \frac{\pi}{6}\ \mbox{ | + | = \frac{\pi}{6}\ \mbox{ rad }</math></li> |
<li><math>\frac{\pi}{8}\ \mbox { radians } | <li><math>\frac{\pi}{8}\ \mbox { radians } | ||
| - | = \frac{\pi}{8} \cdot (1 \; \mbox{ | + | = \frac{\pi}{8} \cdot (1 \; \mbox{rad}\,) |
= \frac{\pi}{8} \cdot \frac{180^\circ}{\pi} | = \frac{\pi}{8} \cdot \frac{180^\circ}{\pi} | ||
= 22{,}5^\circ</math></li> | = 22{,}5^\circ</math></li> | ||
| Zeile 66: | Zeile 66: | ||
</div> | </div> | ||
| - | + | Manchmal spricht man von Winkeln die negativ oder größer als <math>360 \, ^{\circ}</math> sind. Dies bedeutet dass ein Punkt am Kreis durch mehreren Winkeln repräsentiert werden kann. | |
<center>{{:4.1 - Bild - Die Winkeln 45°, -315° und 405°}}</center> | <center>{{:4.1 - Bild - Die Winkeln 45°, -315° und 405°}}</center> | ||
| Zeile 74: | Zeile 74: | ||
<ol type="a"> | <ol type="a"> | ||
| - | <li> | + | <li> Die Winkeln <math>-55^\circ</math> und <math>665^\circ |
| - | </math> | + | </math> repräsentieren denselben Punkt nachdem |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
-55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}</math>}}</li> | -55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}</math>}}</li> | ||
| - | <li> | + | <li> Die Winkeln <math>\frac{3\pi}{7}</math> und <math> |
| - | -\frac{11\pi}{7}</math> | + | -\frac{11\pi}{7}</math> repräsentieren denselben Punkt nachdem |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}</math>}}</li> | \frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}</math>}}</li> | ||
| - | <li> | + | <li> Die Winkeln <math>36^\circ</math> und <math> |
| - | 216^\circ</math> | + | 216^\circ</math> repräsentieren nicht denselben Punkt nachdem |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
36^\circ + 180^\circ = 216^\circ\,\mbox{.}</math>}}</li> | 36^\circ + 180^\circ = 216^\circ\,\mbox{.}</math>}}</li> | ||
| Zeile 92: | Zeile 92: | ||
| - | == | + | == Abstand zwischen zwei Punkten == |
| - | + | Der Satz des Pythagoras ist einer der Berühmtesten Sätze der Mathematik. Der Satz des Pythagoras sagt dass wenn <math>a</math> und <math>b</math> die Katheten eines rechtwinkligen Dreiecks sind, und <math>c</math> die Hypotenuse eines Dreiecks ist, dann ist | |
<div class="regel"> | <div class="regel"> | ||
{|width="100%" | {|width="100%" | ||
| - | |width="100%"|''' | + | |width="100%"|'''Satz des Pythagoras:''' |
{{Abgesetzte Formel||<math>c^2 = a^2 + b^2\,\mbox{.}</math>}} | {{Abgesetzte Formel||<math>c^2 = a^2 + b^2\,\mbox{.}</math>}} | ||
|align="right"|{{:4.1 - Bild - Satz des Pythagoras}} | |align="right"|{{:4.1 - Bild - Satz des Pythagoras}} | ||
| Zeile 108: | Zeile 108: | ||
{| width="100%" | {| width="100%" | ||
| - | |width="100%"| | + | |width="100%"| Wir erhalten c durch den Satz des Pythagoras: |
{{Abgesetzte Formel||<math>c^2= 3^2 + 4^2 = 9 +16 = 25</math>}} | {{Abgesetzte Formel||<math>c^2= 3^2 + 4^2 = 9 +16 = 25</math>}} | ||
| - | + | und deshalb ist | |
{{Abgesetzte Formel||<math>c=\sqrt{25} = 5\,\mbox{.}</math>}} | {{Abgesetzte Formel||<math>c=\sqrt{25} = 5\,\mbox{.}</math>}} | ||
|align="right"|{{:4.1 - Bild - Ein rechteckiges Dreieck mit den Seiten 3, 4 und 5}} | |align="right"|{{:4.1 - Bild - Ein rechteckiges Dreieck mit den Seiten 3, 4 und 5}} | ||
| Zeile 116: | Zeile 116: | ||
</div> | </div> | ||
| - | + | Der Satz des Pythagoras kann verwendet werden um den Abstand zwischen zwei Punkten zu bestimmen. | |
<div class="regel"> | <div class="regel"> | ||
| - | ''' | + | '''Abstand zwischen zwei Punkten:''' |
| - | + | Der Abstand <math>d</math> zwischen den Punkten <math>(x,y)</math> und <math>(a,b)</math> ist | |
{{Abgesetzte Formel||<math>d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}</math>}} | {{Abgesetzte Formel||<math>d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}</math>}} | ||
</div> | </div> | ||
| - | + | Die Gerade zwischen den beiden Punkten ist die Hypotenuse eines Dreiecks wo die Katheten parallel mit den Koordinatenachsen sind. | |
<center>{{:4.1 - Bild - Die Abstandsformel}}</center> | <center>{{:4.1 - Bild - Die Abstandsformel}}</center> | ||
| - | + | Die Katheten des Dreiecks sind die Unterschiede in der ''x''- und ''y''-Richtung für die Punkte, also <math>|x-a|</math> und <math>|y-b|</math>. Durch den Satz des Pythagoras erhalten wir den Abstand zwischen den Punkten. | |
<div class="exempel"> | <div class="exempel"> | ||
| Zeile 134: | Zeile 134: | ||
<ol type="a"> | <ol type="a"> | ||
| - | <li> | + | <li>Der Abstand zwischen <math>(1,2)</math> und <math>(3,1)</math> ist |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
d = \sqrt{ (1-3)^2 + (2-1)^2} | d = \sqrt{ (1-3)^2 + (2-1)^2} | ||
| Zeile 141: | Zeile 141: | ||
= \sqrt{5}\,\mbox{.}</math>}}</li> | = \sqrt{5}\,\mbox{.}</math>}}</li> | ||
| - | <li> | + | <li>Der Abstand zwischen <math>(-1,0)</math> und <math>(-2,-5)</math> ist |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2} | d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2} | ||
| Zeile 151: | Zeile 151: | ||
| - | == | + | == Kreise == |
| - | + | Ein Kreis besteht aus allen Punkten die auf den Abstand <math>r</math> von einen Punkt <math>(a,b)</math> liegen. | |
<center>{{:4.1 - Bild - Kreis}}</center> | <center>{{:4.1 - Bild - Kreis}}</center> | ||
| - | + | Der Abstand <math>r</math> ist der Radius des Kreises, und der punkt <math>(a,b)</math> ist der Mittelpunkt des Kreises. Das Bild zeigt andere Wichtige Begriffe eines Kreises. | |
| - | + | ||
{| align="center" | {| align="center" | ||
| Zeile 200: | Zeile 199: | ||
{| width="100%" | {| width="100%" | ||
| - | || | + | ||Ein Kreisbogen ist in der Figur eingezeichnet. |
<ol type="a"> | <ol type="a"> | ||
| - | <li> | + | <li> Bestimmen Sie die Länge des Kreisbogens |
<br> | <br> | ||
<br> | <br> | ||
| - | + | Der Winkel <math>50^\circ</math> ist in Radianten | |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
50^\circ = 50 \cdot 1^\circ | 50^\circ = 50 \cdot 1^\circ | ||
| - | = 50 \cdot \frac{\pi}{180}\ \mbox{ | + | = 50 \cdot \frac{\pi}{180}\ \mbox{ rad } |
| - | = \frac{5\pi}{18}\ \mbox{ | + | = \frac{5\pi}{18}\ \mbox{ rad. }</math>}} |
</li> | </li> | ||
</ol> | </ol> | ||
| Zeile 216: | Zeile 215: | ||
|} | |} | ||
<ol style="list-style-type:none; padding-top:0; margin-top:0;"> | <ol style="list-style-type:none; padding-top:0; margin-top:0;"> | ||
| - | <li> | + | <li>Laut Definition des Radianten, ist die Länge des Kreisbogens, der Winkel in Radianten multipliziert mit den Radius, |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
3 \cdot \frac{5\pi}{18}\ \mbox{units } | 3 \cdot \frac{5\pi}{18}\ \mbox{units } | ||
| - | = \frac{5\pi}{6}\ \mbox{ | + | = \frac{5\pi}{6}\ \mbox{ Einheiten . }</math>}}</li> |
</ol> | </ol> | ||
<ol type="a" start="2"> | <ol type="a" start="2"> | ||
| - | <li> | + | <li>Bestimmen sie die Fläche des Kreissektors |
<br> | <br> | ||
<br> | <br> | ||
| - | + | Der Kreissektor nimmt den Anteil | |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
\frac{50^\circ}{360^\circ} = \frac{5}{36}</math>}} | \frac{50^\circ}{360^\circ} = \frac{5}{36}</math>}} | ||
| - | + | der Fläche des Kreises auf. Deshalb ist die Fläche des Kreissektors <math>\frac{5}{36}</math> von der ganzen Fläche des Kreises, welche <math>\pi r^2 = \pi 3^2 = 9\pi</math> ist. Also ist die Fläche des Kreissektors | |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
| - | \frac{5}{36} \cdot 9\pi\ \mbox{ | + | \frac{5}{36} \cdot 9\pi\ \mbox{ Einheiten }= \frac{5\pi}{4}\ \mbox{ Einheiten. }</math>}}</li> |
</ol> | </ol> | ||
</div> | </div> | ||
| - | + | Die Punkte <math>(x,y)</math> die auf den Kreis mit dem Mittelpunkt <math>(a,b)</math> und mit dem Radius <math>r</math> liegen, können durch die Formel für den Abstand zwischen zwei Punkten beschrieben werden. | |
<div class="regel"> | <div class="regel"> | ||
{| width="100%" | {| width="100%" | ||
| - | ||''' | + | ||'''Die Gleichung eines Kreises: ''' |
{{Abgesetzte Formel||<math>(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}</math>}} | {{Abgesetzte Formel||<math>(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}</math>}} | ||
|align="right"|{{:4.1 - Bild - Gleichung eines Kreises}} | |align="right"|{{:4.1 - Bild - Gleichung eines Kreises}} | ||
| Zeile 249: | Zeile 248: | ||
|width="100%"| | |width="100%"| | ||
<ol type="a"> | <ol type="a"> | ||
| - | <li><math>(x-1)^2 + (y-2)^2 = 9\quad</math> | + | <li><math>(x-1)^2 + (y-2)^2 = 9\quad</math> ist die Gleichung eines Kreises mit dem Mittelpunkt <math>(1,2)</math> und dem Radius <math>\sqrt{9} = 3</math>.</li> |
</ol> | </ol> | ||
|align="right"|{{:4.1 - Bild - Die Gleichung (x - 1)² + (y - 2)² = 9}} | |align="right"|{{:4.1 - Bild - Die Gleichung (x - 1)² + (y - 2)² = 9}} | ||
| Zeile 255: | Zeile 254: | ||
|width="100%"| | |width="100%"| | ||
<ol type="a" start=2> | <ol type="a" start=2> | ||
| - | <li><math>x^2 + (y-1)^2 = 1\quad</math> | + | <li><math>x^2 + (y-1)^2 = 1\quad</math> ist <math>(x-0)^2 + (y-1)^2 = 1</math> und ist also die Gleichung eines Kreises mit dem Mittelpunkt <math>(0,1)</math> und dem Radius <math>\sqrt{1} = 1</math>.</li> |
</ol> | </ol> | ||
|align="right"|{{:4.1 - Bild - Die Gleichung x² + (y - 1)² = 1}} | |align="right"|{{:4.1 - Bild - Die Gleichung x² + (y - 1)² = 1}} | ||
| Zeile 261: | Zeile 260: | ||
|width="100%"| | |width="100%"| | ||
<ol type="a" start=3> | <ol type="a" start=3> | ||
| - | <li><math>(x+1)^2 + (y-3)^2 = 5\quad</math> | + | <li><math>(x+1)^2 + (y-3)^2 = 5\quad</math> ist <math>(x-(-1))^2 + (y-3)^2 = 5</math> und also die Gleichung eines Kreises mit dem Mittelpunkt <math>(-1,3)</math> und dem Radius <math>\sqrt{5} \approx 2\textrm{.}236</math>.</li> |
</ol> | </ol> | ||
|align="right"|{{:4.1 - Bild - Die Gleichung (x + 1)² + (y - 3)² = 5}} | |align="right"|{{:4.1 - Bild - Die Gleichung (x + 1)² + (y - 3)² = 5}} | ||
| Zeile 271: | Zeile 270: | ||
<ol type="a"> | <ol type="a"> | ||
| - | <li> | + | <li> Liegt der Punkt <math>(1,2)</math> auf dem Kreis <math>(x-4)^2 +y^2=13</math>? |
<br> | <br> | ||
<br> | <br> | ||
| - | + | Wir kontrollieren ob <math>x=1</math> und <math>y=2</math> die Gleichung des Kreises Erfüllen | |
{{Abgesetzte Formel||<math>\begin{align*} | {{Abgesetzte Formel||<math>\begin{align*} | ||
| - | \mbox{ | + | \mbox{Linke Seite } &= (1-4)^2+2^2\\ |
| - | &= (-3)^2+2^2 = 9+4 = 13 = \mbox{ | + | &= (-3)^2+2^2 = 9+4 = 13 = \mbox{Rechte Seite}\,\mbox{.} |
\end{align*}</math>}} | \end{align*}</math>}} | ||
| - | + | Nachdem der Punkt die Gleichung des Kreises erfüllt, liegt er auf dem Kreis. | |
<center>{{:4.1 - Bild - Die Gleichung (x - 4)² + y² = 13}}</center></li> | <center>{{:4.1 - Bild - Die Gleichung (x - 4)² + y² = 13}}</center></li> | ||
| - | <li> | + | <li> Bestimmen Sie die Gleichung für den Kreis der den Mittelpunkt <math>(3,4)</math> hat, und durch den Punkt <math>(1,0)</math> geht. |
<br> | <br> | ||
<br> | <br> | ||
| - | + | Nachdem der Punkt <math>(1,0)</math> auf dem Kreis liegt, muss der Abstand zwischen diesen Punkt und dem Mittelpunkt <math>(3,4)</math>, der Radius des Kreises sein. Also haben wir | |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}</math>}} | c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}</math>}} | ||
| - | + | Und die Gleichung des Kreises ist daher | |
{{Abgesetzte Formel||<math>(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}</math>}} | {{Abgesetzte Formel||<math>(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}</math>}} | ||
<center>{{:4.1 - Bild - Die Gleichung (x - 3)² + (y - 4)² = 20}}</center></li> | <center>{{:4.1 - Bild - Die Gleichung (x - 3)² + (y - 4)² = 20}}</center></li> | ||
| Zeile 298: | Zeile 297: | ||
''' Beispiel 8''' | ''' Beispiel 8''' | ||
| - | + | Bestimmen Sie den Mittelpunkt und Radius des Kreises mit der Gleichung <math>\ x^2 + y^2 – 2x + 4y + 1 = 0</math>. | |
| - | + | Wir wollen die Gleichung des Kreises auf der Form | |
{{Abgesetzte Formel||<math>(x – a)^2 + (y – b)^2 = r^2</math>}} | {{Abgesetzte Formel||<math>(x – a)^2 + (y – b)^2 = r^2</math>}} | ||
| - | + | bringen. Dann können wir den Mittelpunkt direkt als <math>(a,b)</math> ablesen, und den Radius als <math>r</math>. | |
| - | + | Wir benutzen zuerst quadratische Ergänzung für alle <math>x</math>-Terme auf der linken Seite | |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
\underline{x^2-2x\vphantom{(}} + y^2+4y + 1 | \underline{x^2-2x\vphantom{(}} + y^2+4y + 1 | ||
= \underline{(x-1)^2-1^2} + y^2+4y + 1</math>}} | = \underline{(x-1)^2-1^2} + y^2+4y + 1</math>}} | ||
| - | ( | + | (Wir haben nur die unterstrichenen Terme manipuliert) |
| - | + | Jetzt benutzen wir quadratische Ergänzung für alle <math>y</math>-Terme | |
{{Abgesetzte Formel||<math> | {{Abgesetzte Formel||<math> | ||
(x-1)^2-1^2 + \underline{y^2+4y} + 1 | (x-1)^2-1^2 + \underline{y^2+4y} + 1 | ||
= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}</math>}} | = (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}</math>}} | ||
| - | + | Die Linke Seite ist also | |
| - | + | ||
{{Abgesetzte Formel||<math> (x-1)^2 + (y+2)^2-4 </math>}} | {{Abgesetzte Formel||<math> (x-1)^2 + (y+2)^2-4 </math>}} | ||
| - | + | Wenn wir 4 zu beiden Seiten addieren erhalten wir | |
{{Abgesetzte Formel||<math> (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}</math>}} | {{Abgesetzte Formel||<math> (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}</math>}} | ||
| - | + | Also hat der Kreis den Mittelpunkt <math>(1,-2)</math>, und den Radius <math>\sqrt{4}= 2</math>. | |
<center>{{:4.1 - Bild - Die Gleichung x² + y² - 2x + 4y + 1 = 0}}</center> | <center>{{:4.1 - Bild - Die Gleichung x² + y² - 2x + 4y + 1 = 0}}</center> | ||
| Zeile 331: | Zeile 329: | ||
<div class="inforuta" style="width:580px;"> | <div class="inforuta" style="width:580px;"> | ||
| - | '''Tipps fürs | + | '''Tipps fürs Lernen''' |
'''Diagnostische Prüfung und Schlussprüfung''' | '''Diagnostische Prüfung und Schlussprüfung''' | ||
| - | Nachdem | + | Nachdem Sie mit der Theorie fertig sind, sollten Sie die diagnostische Prüfung und die Schlussprüfung machen. Sie finden die links zu den Prüfungen in Ihrer "Student Lounge". |
| - | ''' | + | '''Bedenken Sie folgendes:''' |
Version vom 16:47, 28. Mär. 2009
| Theorie | Übungen |
Inhalt:
- Various angle measures (degrees, radians and revolutions)
- The Pythagorean theorem
- Formula for distance in the plane
- Equation of a circle
Lernziele:
Nach diesem Abschnitt sollten Sie folgendes können :
- To convert between degrees, radians and revolutions.
- To calculate the area and circumference of sectors of a circle.
- The concepts of right-angled triangles including its legs and hypotenuse.
- To formulate and use the Pythagorean theorem.
- To calculate the distance between two points in the plane.
- To sketch circles by completing the square in their equations.
- The concepts of unit circle, tangent, radius, diameter, circumference, chord and arc.
- To solve geometric problems that contain circles.
Winkeleinheiten
Es gibt viele verschiedene Winkeleinheiten, die in verschiedenen Gebieten verwendet werden. Die zwei häufigsten sind Grad und Radiant.
- Grad. Wenn man einen Kreis in 360 gleich große Stücke aufteilt, hat ein Stück den Winkel. Man bezeichnet die Einheit Grad mit \displaystyle {}^\circ.
- Radiant. Eine andere Winkeleinheit ist der Radiant. Der Radiant wird oft rad geschrieben. Ein Radiant wird definiert dadurch dass ein Kreis den Winkel \displaystyle 2\pi rad hat.
Ein Vollreis besteht aus \displaystyle 360^\circ oder \displaystyle 2\pi rad, und also ist
\displaystyle \begin{align*}
&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians }
= \frac{\pi}{180}\ \mbox{ radians,}\\
&1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ
= \frac{180^\circ}{\pi}\,\mbox{.}
\end{align*}
|
Mit diesen Verhältnis kann man Winkeln zwischen den Einheiten Grad und Radiant umwandeln.
Beispiel 1
- \displaystyle 30^\circ = 30 \cdot 1^\circ = 30 \cdot \frac{\pi}{180}\ \mbox{ rad } = \frac{\pi}{6}\ \mbox{ rad }
- \displaystyle \frac{\pi}{8}\ \mbox { radians } = \frac{\pi}{8} \cdot (1 \; \mbox{rad}\,) = \frac{\pi}{8} \cdot \frac{180^\circ}{\pi} = 22{,}5^\circ
Manchmal spricht man von Winkeln die negativ oder größer als \displaystyle 360 \, ^{\circ} sind. Dies bedeutet dass ein Punkt am Kreis durch mehreren Winkeln repräsentiert werden kann.
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/a/d/b/adb5d2a7377ac4e092456d9ca65e66a3.png)
Beispiel 2
- Die Winkeln \displaystyle -55^\circ und \displaystyle 665^\circ
repräsentieren denselben Punkt nachdem
\displaystyle -55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.} - Die Winkeln \displaystyle \frac{3\pi}{7} und \displaystyle
-\frac{11\pi}{7} repräsentieren denselben Punkt nachdem
\displaystyle \frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.} - Die Winkeln \displaystyle 36^\circ und \displaystyle
216^\circ repräsentieren nicht denselben Punkt nachdem
\displaystyle 36^\circ + 180^\circ = 216^\circ\,\mbox{.}
Abstand zwischen zwei Punkten
Der Satz des Pythagoras ist einer der Berühmtesten Sätze der Mathematik. Der Satz des Pythagoras sagt dass wenn \displaystyle a und \displaystyle b die Katheten eines rechtwinkligen Dreiecks sind, und \displaystyle c die Hypotenuse eines Dreiecks ist, dann ist
Satz des Pythagoras:
|
|
Beispiel 3
Wir erhalten c durch den Satz des Pythagoras:
und deshalb ist
|
|
Der Satz des Pythagoras kann verwendet werden um den Abstand zwischen zwei Punkten zu bestimmen.
Abstand zwischen zwei Punkten:
Der Abstand \displaystyle d zwischen den Punkten \displaystyle (x,y) und \displaystyle (a,b) ist
| \displaystyle d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.} |
Die Gerade zwischen den beiden Punkten ist die Hypotenuse eines Dreiecks wo die Katheten parallel mit den Koordinatenachsen sind.
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/b/2/6/b26ce49791aa401bb74412d49e5ba4f4.png)
Die Katheten des Dreiecks sind die Unterschiede in der x- und y-Richtung für die Punkte, also \displaystyle |x-a| und \displaystyle |y-b|. Durch den Satz des Pythagoras erhalten wir den Abstand zwischen den Punkten.
Beispiel 4
- Der Abstand zwischen \displaystyle (1,2) und \displaystyle (3,1) ist
\displaystyle d = \sqrt{ (1-3)^2 + (2-1)^2} = \sqrt{(-2)^2 + 1^2} = \sqrt{ 4+1} = \sqrt{5}\,\mbox{.} - Der Abstand zwischen \displaystyle (-1,0) und \displaystyle (-2,-5) ist
\displaystyle d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2} = \sqrt{1^2 + 5^2} = \sqrt{1+25} = \sqrt{26}\,\mbox{.}
Kreise
Ein Kreis besteht aus allen Punkten die auf den Abstand \displaystyle r von einen Punkt \displaystyle (a,b) liegen.
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/0/6/2/06282cc22b3fe6eeea36613925ce586b.png)
Der Abstand \displaystyle r ist der Radius des Kreises, und der punkt \displaystyle (a,b) ist der Mittelpunkt des Kreises. Das Bild zeigt andere Wichtige Begriffe eines Kreises.
|
|
|
|
| |||
| Diameter | Tangent | Chord | Secant | |||
|
|
|
|
| |||
| Arc of a circle | circumference | sector of a circle | segment of a circle |
Beispiel 5
Ein Kreisbogen ist in der Figur eingezeichnet.
|
|
- Laut Definition des Radianten, ist die Länge des Kreisbogens, der Winkel in Radianten multipliziert mit den Radius,
\displaystyle 3 \cdot \frac{5\pi}{18}\ \mbox{units } = \frac{5\pi}{6}\ \mbox{ Einheiten . }
- Bestimmen sie die Fläche des Kreissektors
Der Kreissektor nimmt den Anteil\displaystyle \frac{50^\circ}{360^\circ} = \frac{5}{36}der Fläche des Kreises auf. Deshalb ist die Fläche des Kreissektors \displaystyle \frac{5}{36} von der ganzen Fläche des Kreises, welche \displaystyle \pi r^2 = \pi 3^2 = 9\pi ist. Also ist die Fläche des Kreissektors
\displaystyle \frac{5}{36} \cdot 9\pi\ \mbox{ Einheiten }= \frac{5\pi}{4}\ \mbox{ Einheiten. }
Die Punkte \displaystyle (x,y) die auf den Kreis mit dem Mittelpunkt \displaystyle (a,b) und mit dem Radius \displaystyle r liegen, können durch die Formel für den Abstand zwischen zwei Punkten beschrieben werden.
Die Gleichung eines Kreises:
|
|
Beispiel 6
|
|
|
|
|
|
Beispiel 7
- Liegt der Punkt \displaystyle (1,2) auf dem Kreis \displaystyle (x-4)^2 +y^2=13?
Wir kontrollieren ob \displaystyle x=1 und \displaystyle y=2 die Gleichung des Kreises Erfüllen\displaystyle \begin{align*} \mbox{Linke Seite } &= (1-4)^2+2^2\\ &= (-3)^2+2^2 = 9+4 = 13 = \mbox{Rechte Seite}\,\mbox{.} \end{align*}Nachdem der Punkt die Gleichung des Kreises erfüllt, liegt er auf dem Kreis.
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/c/2/b/c2b604362bebb4cb5d5959a822a50d9b.png)
- Bestimmen Sie die Gleichung für den Kreis der den Mittelpunkt \displaystyle (3,4) hat, und durch den Punkt \displaystyle (1,0) geht.
Nachdem der Punkt \displaystyle (1,0) auf dem Kreis liegt, muss der Abstand zwischen diesen Punkt und dem Mittelpunkt \displaystyle (3,4), der Radius des Kreises sein. Also haben wir\displaystyle c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}Und die Gleichung des Kreises ist daher
\displaystyle (x-3)^2 + (y-4)^2 = 20 \; \mbox{.} ![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/2/e/7/2e78c8b92478416492f4a0953246469b.png)
Beispiel 8
Bestimmen Sie den Mittelpunkt und Radius des Kreises mit der Gleichung \displaystyle \ x^2 + y^2 – 2x + 4y + 1 = 0.
Wir wollen die Gleichung des Kreises auf der Form
| \displaystyle (x – a)^2 + (y – b)^2 = r^2 |
bringen. Dann können wir den Mittelpunkt direkt als \displaystyle (a,b) ablesen, und den Radius als \displaystyle r.
Wir benutzen zuerst quadratische Ergänzung für alle \displaystyle x-Terme auf der linken Seite
\displaystyle
\underline{x^2-2x\vphantom{(}} + y^2+4y + 1
= \underline{(x-1)^2-1^2} + y^2+4y + 1
|
(Wir haben nur die unterstrichenen Terme manipuliert)
Jetzt benutzen wir quadratische Ergänzung für alle \displaystyle y-Terme
\displaystyle
(x-1)^2-1^2 + \underline{y^2+4y} + 1
= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}
|
Die Linke Seite ist also
| \displaystyle (x-1)^2 + (y+2)^2-4 |
Wenn wir 4 zu beiden Seiten addieren erhalten wir
| \displaystyle (x-1)^2 + (y+2)^2 = 4 \, \mbox{.} |
Also hat der Kreis den Mittelpunkt \displaystyle (1,-2), und den Radius \displaystyle \sqrt{4}= 2.
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/7/b/2/7b2d3a06ca4d11646449b1541cdab526.png)
Tipps fürs Lernen
Diagnostische Prüfung und Schlussprüfung
Nachdem Sie mit der Theorie fertig sind, sollten Sie die diagnostische Prüfung und die Schlussprüfung machen. Sie finden die links zu den Prüfungen in Ihrer "Student Lounge".
Bedenken Sie folgendes:
Reviews
For those of you who want to deepen your studies or need more detailed explanations consider the following references:
Learn more about Pythagoras theorem in English Wikipedia
Read more in Mathworld about the circle
Nützliche Websites
Interactive experiments: the sine and cosine on the unit circle (Flash)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/7/2/9/7297c9bc30e68c93394025b132182670.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/d/2/f/d2ff7df26ceb7ecc6fab9646b919d9dd.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/8/2/1/821b8a352c39f6b69318c96ec25a84e7.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/2/3/e/23e1cbb7c8b731963ffa4aeda821b277.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/a/2/7/a27e381d480493ba0cb77e460cd17758.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/4/a/5/4a54d959f82763e83e41a86ad60933d2.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/b/2/0/b20d39083d55d8fe6e7454c1815f021b.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/f/a/4/fa48ec8305ef998ba790a540ab326c6f.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/5/c/9/5c9f453cdf00df1693557161cc6fceb4.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/a/f/d/afd624e400bff836280c119ab4cb970a.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/4/7/e/47e696fd84f13fed85b1394795a31875.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/c/1/b/c1b9fe94e84310b947c2f12983ec753d.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/1/a/4/1a4fb90a0e677a995867186eb909f5b5.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/b/2/1/b2185b3d2e88d185bc40539702f21363.png)
![[Image]](/wikis/2009/bridgecourse1-TU-Berlin/img_auth.php/metapost/4/d/e/4de1b674a9d9f670007e817471136f91.png)
