Lösung 2.3:10d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (hat „Solution 2.3:10d“ nach „Lösung 2.3:10d“ verschoben: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | Wir schreiben die doppelte Ungleichung <math>x^2\le y\le x</math> wie <math>x^2\le y</math> und <math>y\le x\,</math>. Diese Ungleichungen definieren das Gebiet oberhalb der Parabel <math>y=x^2</math> und unterhalb der Gerade <math>y=x</math>. | |
| Zeile 7: | Zeile 7: | ||
|align="center"|[[Image:2_3_10_d1-2.gif|center]] | |align="center"|[[Image:2_3_10_d1-2.gif|center]] | ||
|- | |- | ||
| - | |align="center"|<small> | + | |align="center"|<small>Das Gebiet ''x''² ≤ ''y''</small> |
|| | || | ||
| - | |align="center"|<small> | + | |align="center"|<small>Das Gebiet ''y'' ≤ ''x''</small> |
|} | |} | ||
| - | + | Unser Gebiet sind die Punkte die Beide Ungleichungen erfüllen. | |
| - | + | ||
| Zeile 19: | Zeile 18: | ||
|align="center"|[[Image:2_3_10_d2.gif|center]] | |align="center"|[[Image:2_3_10_d2.gif|center]] | ||
|- | |- | ||
| - | |align="center"|<small> | + | |align="center"|<small>Das Gebiet ''x''² ≤ y ≤ x</small> |
|} | |} | ||
Version vom 21:17, 16. Mär. 2009
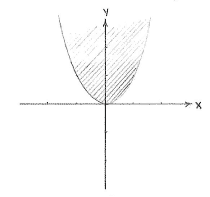
Wir schreiben die doppelte Ungleichung \displaystyle x^2\le y\le x wie \displaystyle x^2\le y und \displaystyle y\le x\,. Diese Ungleichungen definieren das Gebiet oberhalb der Parabel \displaystyle y=x^2 und unterhalb der Gerade \displaystyle y=x.
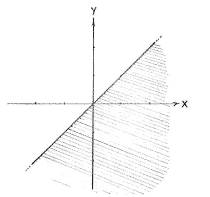
| Das Gebiet x² ≤ y | Das Gebiet y ≤ x |
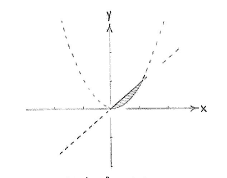
Unser Gebiet sind die Punkte die Beide Ungleichungen erfüllen.
| Das Gebiet x² ≤ y ≤ x |