Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 2.3:9a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 2.3:9a“ nach „Lösung 2.3:9a“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
A point lies on the ''x''-axis if it has ''y''-coordinate 0 and we therefore look for all the points on the curve <math>y=x^{2}-1</math> where <math>y=0</math>, i.e. all points which satisfy the equation
+
Jeder Punkt auf der ''x''-Achse, hat den ''y''.Koordinaten 0, und daher müssen die Schnittpunkte folgende Gleichung erfüllen
{{Abgesetzte Formel||<math>0=x^{2}-1\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>0=x^{2}-1\,\textrm{.}</math>}}
-
This equation has solutions <math>x=\pm 1</math>, which means that the points of intersection are <math>(-1,0)</math> and <math>(1,0)</math>.
+
Diese Gleichung hat die Lösungen <math>x=\pm 1</math>, und also sind die Schnittpunkte <math>(-1,0)</math> und <math>(1,0)</math>.
[[Image:2_3_9_a.gif|center]]
[[Image:2_3_9_a.gif|center]]

Version vom 19:54, 16. Mär. 2009

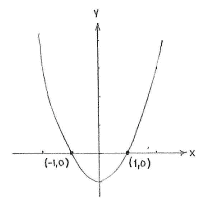
Jeder Punkt auf der x-Achse, hat den y.Koordinaten 0, und daher müssen die Schnittpunkte folgende Gleichung erfüllen

0=x2−1.

Diese Gleichung hat die Lösungen x=1, und also sind die Schnittpunkte (−10) und (10).


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.3:9a“