Aus Online Mathematik Brückenkurs 1

Version vom 13:57, 22. Okt. 2008 (bearbeiten) Tekbot (Diskussion | Beiträge) K (hat „Solution 2.2:5a“ nach „Lösung 2.2:5a“ verschoben: Robot: moved page) ← Zum vorherigen Versionsunterschied		Version vom 17:20, 12. Mär. 2009 (bearbeiten) (rückgängig) Martin (Diskussion | Beiträge) Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
-	Let's write down the equation for a straight line as	+	Die Gleichung einer Geraden lautet
	{{Abgesetzte Formel||<math>y=kx+m\,,</math>}}		{{Abgesetzte Formel||<math>y=kx+m\,,</math>}}
-	where ''k'' and ''m'' are constants which we shall determine.	+	Wir wollen die Konstanten ''k'' und ''m'' bestimmen.
-	Since the points (2,3) and (3,0) should lie on the line, they must also satisfy the equation of the line,	+	Nachdem die Punkte (2,3) und (3,0) auf der Geraden liegen, müssen sie auch die Gleichung der Geraden erfüllen.
	{{Abgesetzte Formel||<math>3=k\cdot 2+m\qquad\text{and}\qquad 0=k\cdot 3+m\,\textrm{.}</math>}}		{{Abgesetzte Formel||<math>3=k\cdot 2+m\qquad\text{and}\qquad 0=k\cdot 3+m\,\textrm{.}</math>}}
-	If we take the difference between the equations, ''m'' disappears and we can work out the slope ''k'',	+	Wenn wir die erste Gleichung von der zweiten subtrahieren, wird ''m'' gekürzt, und wir erhallten ''k''
	{{Abgesetzte Formel||<math>\begin{align}		{{Abgesetzte Formel||<math>\begin{align}
Zeile 16:		Zeile 16:
	\end{align}</math>}}		\end{align}</math>}}
-	Substituting this into the equation <math>0=k\centerdot 3+m</math> then gives us a value for ''m'',	+
		+	Ersetzen wir ''k'' mit -3 in der Gleichung <math>0=k\centerdot 3+m</math>, bekommen wir ''m'',
	{{Abgesetzte Formel||<math>m=-3k=-3\cdot (-3)=9\,\textrm{.}</math>}}		{{Abgesetzte Formel||<math>m=-3k=-3\cdot (-3)=9\,\textrm{.}</math>}}
-	The equation of the line is thus <math>y=-3x+9</math>.	+	Die Gleichung der Geraden ist also <math>y=-3x+9</math>.
Zeile 26:		Zeile 27:
-	Note. To be completely certain that we have calculated correctly, we check that the points (2,3) and (3,0) satisfy the equation of the line:	+	Hinweis: Wir können unsere Lösung testen, indem wir kontrollieren ob die Punkte (2,3) und (3,0) die Gleichung der Geraden erfüllen:
-	:*(''x'',''y'')&nbsp;=&nbsp;(2,3): <math>\text{LHS} = 3\ </math> and <math>\ \text{RHS} = -3\cdot 2+9 = 3\,</math>.	+	:*(''x'',''y'')&nbsp;=&nbsp;(2,3): <math>\text{LHS} = 3\ </math> und <math>\ \text{RHS} = -3\cdot 2+9 = 3\,</math>.
-	:*(''x'',''y'')&nbsp;=&nbsp;(3,0): <math>\text{LHS} = 0\ </math> and <math>\ \text{LHS} = -3\cdot 3+9 = 0\,</math>.	+	:*(''x'',''y'')&nbsp;=&nbsp;(3,0): <math>\text{LHS} = 0\ </math> und <math>\ \text{LHS} = -3\cdot 3+9 = 0\,</math>.

---

Version vom 17:20, 12. Mär. 2009

Die Gleichung einer Geraden lautet

\displaystyle y=kx+m\,,

Wir wollen die Konstanten k und m bestimmen.

Nachdem die Punkte (2,3) und (3,0) auf der Geraden liegen, müssen sie auch die Gleichung der Geraden erfüllen.

\displaystyle 3=k\cdot 2+m\qquad\text{and}\qquad 0=k\cdot 3+m\,\textrm{.}

Wenn wir die erste Gleichung von der zweiten subtrahieren, wird m gekürzt, und wir erhallten k

\displaystyle \begin{align} 3-0 &= k\cdot 2+m-(k\cdot 3+m)\,,\\[5pt] 3 &= -k\,\textrm{.} \end{align}

Ersetzen wir k mit -3 in der Gleichung \displaystyle 0=k\centerdot 3+m, bekommen wir m,

\displaystyle m=-3k=-3\cdot (-3)=9\,\textrm{.}

Die Gleichung der Geraden ist also \displaystyle y=-3x+9.

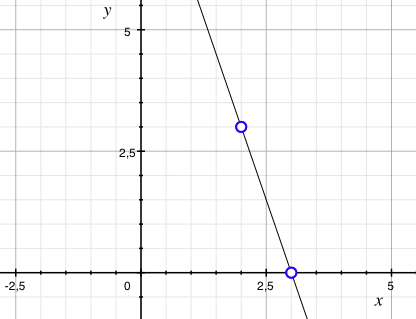
Hinweis: Wir können unsere Lösung testen, indem wir kontrollieren ob die Punkte (2,3) und (3,0) die Gleichung der Geraden erfüllen:

• (x,y) = (2,3): \displaystyle \text{LHS} = 3\ und \displaystyle \ \text{RHS} = -3\cdot 2+9 = 3\,.
• (x,y) = (3,0): \displaystyle \text{LHS} = 0\ und \displaystyle \ \text{LHS} = -3\cdot 3+9 = 0\,.