Lösung 4.2:4e
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
K (hat „Solution 4.2:4e“ nach „Lösung 4.2:4e“ verschoben: Robot: moved page) |
Version vom 14:57, 22. Okt. 2008
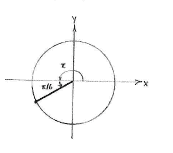
If we write the angle \displaystyle \frac{7\pi}{6} as
| \displaystyle \frac{7\pi}{6} = \frac{6\pi+\pi}{6} = \pi + \frac{\pi }{6} |
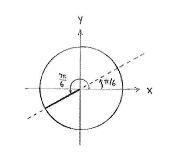
we see that the angle \displaystyle 7\pi/6 on the unit circle is in the third quadrant and makes an angle \displaystyle \pi/6 with the negative x-axis.
Geometrically, \displaystyle \tan (7\pi/6) is defined as the slope of the line having an angle \displaystyle 7\pi/6 and, because this line has the same slope as the line having angle \displaystyle \pi/6, we have that
| \displaystyle \tan\frac{7\pi}{6} = \tan\frac{\pi}{6} = \frac{\sin\dfrac{\pi }{6}}{\cos\dfrac{\pi }{6}} = \frac{\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}}\,\textrm{.} |