Lösung 4.2:3c
Aus Online Mathematik Brückenkurs 1
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
K (hat „Solution 4.2:3c“ nach „Lösung 4.2:3c“ verschoben: Robot: moved page) |
Version vom 14:54, 22. Okt. 2008
We can add and subtract multiples of \displaystyle 2\pi to or from the argument of the sine function without changing its value. The angle \displaystyle 2\pi corresponds to a whole turn in a unit circle and the sine function returns to the same value every time the angle changes by a complete revolution.
For example, if we can subtract sufficiently many \displaystyle 2\pi's from \displaystyle 9\pi, we will obtain a more manageable argument which lies between \displaystyle 0 and \displaystyle 2\pi\,,
| \displaystyle \sin 9\pi = \sin (9\pi - 2\pi - 2\pi - 2\pi - 2\pi) = \sin \pi\,\textrm{.} |
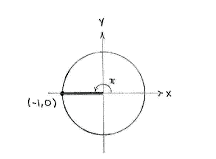
The line which makes an angle \displaystyle \pi with the positive part of the x-axis is the negative part of the x-axis and it cuts the unit circle at the point (-1,0), which is why we can see from the y-coordinate that \displaystyle \sin 9\pi = \sin \pi = 0\,.