Lösung 4.4:5c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
For a fixed value of ''u'', an equality of the form
For a fixed value of ''u'', an equality of the form
-
{{Displayed math||<math>\cos u=\cos v</math>}}
+
{{Abgesetzte Formel||<math>\cos u=\cos v</math>}}
is satisfied by two angles ''v'' in the unit circle,
is satisfied by two angles ''v'' in the unit circle,
-
{{Displayed math||<math>v=u\qquad\text{and}\qquad v=-u\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>v=u\qquad\text{and}\qquad v=-u\,\textrm{.}</math>}}
[[Image:4_4_5_c.gif|center]]
[[Image:4_4_5_c.gif|center]]
Zeile 11: Zeile 11:
This means that all angles ''v'' which satisfy the equality are
This means that all angles ''v'' which satisfy the equality are
-
{{Displayed math||<math>v=u+2n\pi\qquad\text{and}\qquad v=-u+2n\pi\,,</math>}}
+
{{Abgesetzte Formel||<math>v=u+2n\pi\qquad\text{and}\qquad v=-u+2n\pi\,,</math>}}
where ''n'' is an arbitrary integer.
where ''n'' is an arbitrary integer.
Zeile 17: Zeile 17:
Therefore, the equation
Therefore, the equation
-
{{Displayed math||<math>\cos 5x=\cos (x+\pi/5)</math>}}
+
{{Abgesetzte Formel||<math>\cos 5x=\cos (x+\pi/5)</math>}}
has the solutions
has the solutions
-
{{Displayed math||<math>\left\{\begin{align} 5x&=x+\frac{\pi}{5}+2n\pi\quad\text{or}\\[5pt] 5x &= -x-\frac{\pi}{5}+2n\pi\,\textrm{.}\end{align}\right.</math>}}
+
{{Abgesetzte Formel||<math>\left\{\begin{align} 5x&=x+\frac{\pi}{5}+2n\pi\quad\text{or}\\[5pt] 5x &= -x-\frac{\pi}{5}+2n\pi\,\textrm{.}\end{align}\right.</math>}}
If we collect ''x'' onto one side, we end up with
If we collect ''x'' onto one side, we end up with
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
x &= \frac{\pi}{20} + \frac{n\pi}{2}\,,\\[5pt]
x &= \frac{\pi}{20} + \frac{n\pi}{2}\,,\\[5pt]
x &= -\frac{\pi }{30}+\frac{n\pi}{3}\,,
x &= -\frac{\pi }{30}+\frac{n\pi}{3}\,,

Version vom 09:00, 22. Okt. 2008

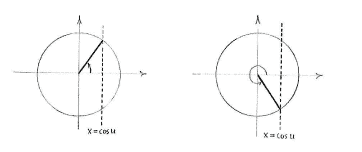
For a fixed value of u, an equality of the form

\displaystyle \cos u=\cos v

is satisfied by two angles v in the unit circle,

\displaystyle v=u\qquad\text{and}\qquad v=-u\,\textrm{.}

This means that all angles v which satisfy the equality are

\displaystyle v=u+2n\pi\qquad\text{and}\qquad v=-u+2n\pi\,,

where n is an arbitrary integer.

Therefore, the equation

\displaystyle \cos 5x=\cos (x+\pi/5)

has the solutions

\displaystyle \left\{\begin{align} 5x&=x+\frac{\pi}{5}+2n\pi\quad\text{or}\\[5pt] 5x &= -x-\frac{\pi}{5}+2n\pi\,\textrm{.}\end{align}\right.

If we collect x onto one side, we end up with

\displaystyle \left\{\begin{align}

x &= \frac{\pi}{20} + \frac{n\pi}{2}\,,\\[5pt] x &= -\frac{\pi }{30}+\frac{n\pi}{3}\,, \end{align}\right.

where n is an arbitrary integer.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:5c“