Lösung 4.4:2b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 5: | Zeile 5: | ||
If we add multiples of <math>2\pi</math> to these two solutions, we obtain all the solutions | If we add multiples of <math>2\pi</math> to these two solutions, we obtain all the solutions | ||
| - | {{ | + | {{Abgesetzte Formel||<math>x = \frac{\pi}{3}+2n\pi\qquad\text{and}\qquad x = \frac{5\pi }{3}+2n\pi\,,</math>}} |
where ''n'' is an arbitrary integer. | where ''n'' is an arbitrary integer. | ||
Version vom 08:58, 22. Okt. 2008
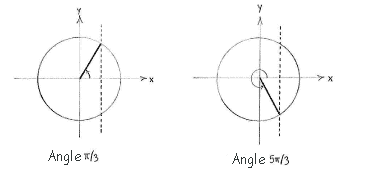
The equation \displaystyle \cos x= 1/2 has the solution \displaystyle x=\pi/3 in the first quadrant, and the symmetric solution \displaystyle x = 2\pi -\pi/3 = 5\pi/3 in the fourth quadrant.
If we add multiples of \displaystyle 2\pi to these two solutions, we obtain all the solutions
| \displaystyle x = \frac{\pi}{3}+2n\pi\qquad\text{and}\qquad x = \frac{5\pi }{3}+2n\pi\,, |
where n is an arbitrary integer.