Lösung 4.4:2a
Aus Online Mathematik Brückenkurs 1
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 8: | Zeile 8: | ||
Each of those solutions returns to itself after every revolution, so that we obtain the complete solution if we add multiples of <math>2\pi</math> | Each of those solutions returns to itself after every revolution, so that we obtain the complete solution if we add multiples of <math>2\pi</math> | ||
| - | {{ | + | {{Abgesetzte Formel||<math>x = \frac{\pi}{3}+2n\pi\qquad\text{and}\qquad x = \frac{2\pi}{3}+2n\pi\,,</math>}} |
where ''n'' is an arbitrary integer. | where ''n'' is an arbitrary integer. | ||
| Zeile 15: | Zeile 15: | ||
Note: When we write that the complete solution is given by | Note: When we write that the complete solution is given by | ||
| - | {{ | + | {{Abgesetzte Formel||<math>x = \frac{\pi}{3}+2n\pi\qquad\text{and}\qquad x = \frac{2\pi}{3}+2n\pi\,\textrm{,}</math>}} |
this means that for every integer ''n'', we obtain a solution to the equation: | this means that for every integer ''n'', we obtain a solution to the equation: | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{array}{llll} |
&n=0:\quad &x=\frac{\pi}{3}\quad &x=\frac{2\pi }{3}\\[5pt] | &n=0:\quad &x=\frac{\pi}{3}\quad &x=\frac{2\pi }{3}\\[5pt] | ||
&n=-1:\quad &x=\frac{\pi}{3}+(-1)\cdot 2\pi\quad &x=\frac{2\pi}{3}+(-1)\cdot 2\pi\\[5pt] | &n=-1:\quad &x=\frac{\pi}{3}+(-1)\cdot 2\pi\quad &x=\frac{2\pi}{3}+(-1)\cdot 2\pi\\[5pt] | ||
Version vom 08:57, 22. Okt. 2008
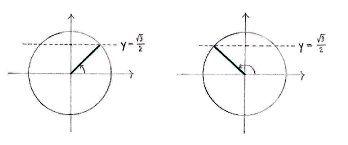
We draw a unit circle and mark those angles on the circle which have a y-coordinate of \displaystyle \sqrt{3}/2, in order to see which solutions lie between \displaystyle 0 and \displaystyle 2\pi.
In the first quadrant, we recognize \displaystyle x = \pi/3 as the angle which has a sine value of \displaystyle \sqrt{3}/2 and then we have the reflectionally symmetric solution \displaystyle x = \pi - \pi/3 = 2\pi/3 in the second quadrant.
Each of those solutions returns to itself after every revolution, so that we obtain the complete solution if we add multiples of \displaystyle 2\pi
| \displaystyle x = \frac{\pi}{3}+2n\pi\qquad\text{and}\qquad x = \frac{2\pi}{3}+2n\pi\,, |
where n is an arbitrary integer.
Note: When we write that the complete solution is given by
| \displaystyle x = \frac{\pi}{3}+2n\pi\qquad\text{and}\qquad x = \frac{2\pi}{3}+2n\pi\,\textrm{,} |
this means that for every integer n, we obtain a solution to the equation:
| \displaystyle \begin{array}{llll}
&n=0:\quad &x=\frac{\pi}{3}\quad &x=\frac{2\pi }{3}\\[5pt] &n=-1:\quad &x=\frac{\pi}{3}+(-1)\cdot 2\pi\quad &x=\frac{2\pi}{3}+(-1)\cdot 2\pi\\[5pt] &n=1:\quad &x=\frac{\pi}{3}+1\cdot 2\pi\quad &x=\frac{2\pi}{3}+1\cdot 2\pi\\[5pt] &n=-2:\quad &x=\frac{\pi}{3}+(-2)\cdot 2\pi\quad &x=\frac{2\pi}{3}+(-2)\cdot 2\pi\\[5pt] &n=2:\quad &x=\frac{\pi}{3}+2\cdot 2\pi\quad &x=\frac{2\pi}{3}+2\cdot 2\pi\\[5pt] &\phantom{n}\vdots &\phantom{x}\vdots &\phantom{x}\vdots \end{array} |