Lösung 4.2:9
Aus Online Mathematik Brückenkurs 1
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 5: | Zeile 5: | ||
One way to determine the hypotenuse is to know the triangle's opposite and adjacent sides, since the Pythagorean theorem then gives | One way to determine the hypotenuse is to know the triangle's opposite and adjacent sides, since the Pythagorean theorem then gives | ||
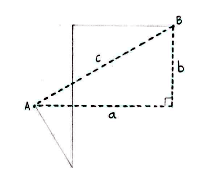
| - | {{ | + | {{Abgesetzte Formel||<math>c^2 = a^2 + b^2\,\textrm{.}</math>}} |
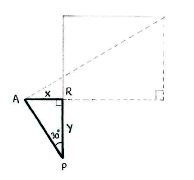
In turn, we can determine the opposite and adjacent by introducing another triangle APR, where R is the point on the line PQ which the dashed triangle's side of length ''a'' cuts the line. | In turn, we can determine the opposite and adjacent by introducing another triangle APR, where R is the point on the line PQ which the dashed triangle's side of length ''a'' cuts the line. | ||
| Zeile 13: | Zeile 13: | ||
Because we know that <math>\text{AP}=4</math> and the angle at P, simple trigonometry shows that ''x'' and ''y'' are given by | Because we know that <math>\text{AP}=4</math> and the angle at P, simple trigonometry shows that ''x'' and ''y'' are given by | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
x &= 4\sin 30^{\circ } = 4\cdot \frac{1}{2} = 2,\\[5pt] | x &= 4\sin 30^{\circ } = 4\cdot \frac{1}{2} = 2,\\[5pt] | ||
y &= 4\cos 30^{\circ } = 4\cdot \frac{\sqrt{3}}{2} = 2\sqrt{3}\,\textrm{.} | y &= 4\cos 30^{\circ } = 4\cdot \frac{\sqrt{3}}{2} = 2\sqrt{3}\,\textrm{.} | ||
| Zeile 32: | Zeile 32: | ||
With ''a'' and ''b'' given, the Pythagorean theorem leads to | With ''a'' and ''b'' given, the Pythagorean theorem leads to | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
c &= \sqrt{a^2+b^2}\\[5pt] | c &= \sqrt{a^2+b^2}\\[5pt] | ||
&= \sqrt{7^2+(12-2\sqrt{3})^2}\\[5pt] | &= \sqrt{7^2+(12-2\sqrt{3})^2}\\[5pt] | ||
Version vom 08:53, 22. Okt. 2008
If we introduce the dashed triangle below, the distance as the crow flies between A and B is equal to the triangle's hypotenuse, c.
One way to determine the hypotenuse is to know the triangle's opposite and adjacent sides, since the Pythagorean theorem then gives
| \displaystyle c^2 = a^2 + b^2\,\textrm{.} |
In turn, we can determine the opposite and adjacent by introducing another triangle APR, where R is the point on the line PQ which the dashed triangle's side of length a cuts the line.
Because we know that \displaystyle \text{AP}=4 and the angle at P, simple trigonometry shows that x and y are given by
| \displaystyle \begin{align}
x &= 4\sin 30^{\circ } = 4\cdot \frac{1}{2} = 2,\\[5pt] y &= 4\cos 30^{\circ } = 4\cdot \frac{\sqrt{3}}{2} = 2\sqrt{3}\,\textrm{.} \end{align} |
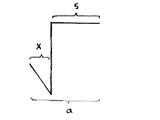
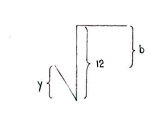
We can now start to look for the solution. Since x and y have been calculated, we can determine a and b by considering the horizontal and vertical distances in the figure.
| 
| |
| \displaystyle \begin{align}a &= x+5\\ &= 2+5 = 7\end{align} | \displaystyle \begin{align}b &= 12-y\\ &= 12-2\sqrt{3}\end{align} |
With a and b given, the Pythagorean theorem leads to
| \displaystyle \begin{align}
c &= \sqrt{a^2+b^2}\\[5pt] &= \sqrt{7^2+(12-2\sqrt{3})^2}\\[5pt] &= \sqrt{49+(12^2-2\cdot 12\cdot 2\sqrt{3}+(2\sqrt{3})^2)}\\[5pt] &= \sqrt{205-38\sqrt{3}}\\[5pt] &\approx 11\textrm{.}0\ \text{km}\textrm{.} \end{align} |