Aus Online Mathematik Brückenkurs 1

Version vom 12:23, 9. Okt. 2008 (bearbeiten) Tek (Diskussion | Beiträge) K ← Zum vorherigen Versionsunterschied		Version vom 08:53, 22. Okt. 2008 (bearbeiten) (rückgängig) Tekbot (Diskussion | Beiträge) K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) Zum nächsten Versionsunterschied →
Zeile 5:		Zeile 5:
	Using the definition of cosine, we can work out ''x'' and ''y'' from		Using the definition of cosine, we can work out ''x'' and ''y'' from
-	{{Displayed math||<math>\begin{align}	+	{{Abgesetzte Formel||<math>\begin{align}
	x &= a\cos \alpha\,,\\[3pt]		x &= a\cos \alpha\,,\\[3pt]
	y &= b\cos \beta\,,		y &= b\cos \beta\,,
Zeile 12:		Zeile 12:
	and, for the same reason, we know that ''z'' satisfies the relation		and, for the same reason, we know that ''z'' satisfies the relation
-	{{Displayed math||<math>z=\ell\cos \gamma\,\textrm{.}</math>}}	+	{{Abgesetzte Formel||<math>z=\ell\cos \gamma\,\textrm{.}</math>}}
	In addition, we know that the lengths ''x'', ''y'' and ''z'' satisfy the equality		In addition, we know that the lengths ''x'', ''y'' and ''z'' satisfy the equality
-	{{Displayed math||<math>z=x-y\,\textrm{.}</math>}}	+	{{Abgesetzte Formel||<math>z=x-y\,\textrm{.}</math>}}
	If we substitute in the expressions for ''x'', ''y'' and ''z'', we obtain the trigonometric equation		If we substitute in the expressions for ''x'', ''y'' and ''z'', we obtain the trigonometric equation
-	{{Displayed math||<math>\ell\cos \gamma = a\cos \alpha -b\cos \beta\,\textrm{,}</math>}}	+	{{Abgesetzte Formel||<math>\ell\cos \gamma = a\cos \alpha -b\cos \beta\,\textrm{,}</math>}}
	where <math>\gamma </math> is the only unknown.		where <math>\gamma </math> is the only unknown.

---

Version vom 08:53, 22. Okt. 2008

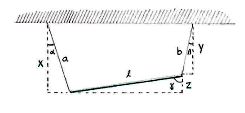
We start by drawing three auxiliary triangles, and calling the three vertical sides x, y and z, as shown in the figure.

Using the definition of cosine, we can work out x and y from

\displaystyle \begin{align} x &= a\cos \alpha\,,\\[3pt] y &= b\cos \beta\,, \end{align}

and, for the same reason, we know that z satisfies the relation

\displaystyle z=\ell\cos \gamma\,\textrm{.}

In addition, we know that the lengths x, y and z satisfy the equality

\displaystyle z=x-y\,\textrm{.}

If we substitute in the expressions for x, y and z, we obtain the trigonometric equation

\displaystyle \ell\cos \gamma = a\cos \alpha -b\cos \beta\,\textrm{,}

where \displaystyle \gamma is the only unknown.