Lösung 4.2:5b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 5: Zeile 5:
This means that <math>\tan 225^{\circ}</math>, which is the slope of the line that makes an angle of <math>45^{\circ}</math> with the positive ''x''-axis, equals <math>\tan 45^{\circ}</math>, because the line which makes an angle of <math>45^{\circ}</math> has the same slope,
This means that <math>\tan 225^{\circ}</math>, which is the slope of the line that makes an angle of <math>45^{\circ}</math> with the positive ''x''-axis, equals <math>\tan 45^{\circ}</math>, because the line which makes an angle of <math>45^{\circ}</math> has the same slope,
-
{{Displayed math||<math>\tan 225^{\circ} = \tan 45^{\circ} = \frac{\sin 45^{\circ}}{\cos 45^{\circ}} = \frac{\dfrac{1}{\sqrt{2}}}{\dfrac{1}{\sqrt{2}}} = 1\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>\tan 225^{\circ} = \tan 45^{\circ} = \frac{\sin 45^{\circ}}{\cos 45^{\circ}} = \frac{\dfrac{1}{\sqrt{2}}}{\dfrac{1}{\sqrt{2}}} = 1\,\textrm{.}</math>}}
[[Image:4_2_5_b2.gif|center]]
[[Image:4_2_5_b2.gif|center]]

Version vom 08:52, 22. Okt. 2008

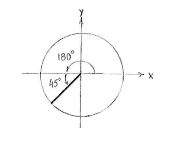
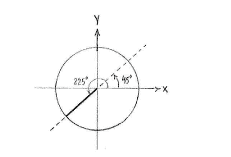
If we draw the angle \displaystyle 225^{\circ} = 180^{\circ} + 45^{\circ} on a unit circle, we see that it makes an angle of \displaystyle 45^{\circ} with the negative x-axis.

This means that \displaystyle \tan 225^{\circ}, which is the slope of the line that makes an angle of \displaystyle 45^{\circ} with the positive x-axis, equals \displaystyle \tan 45^{\circ}, because the line which makes an angle of \displaystyle 45^{\circ} has the same slope,

\displaystyle \tan 225^{\circ} = \tan 45^{\circ} = \frac{\sin 45^{\circ}}{\cos 45^{\circ}} = \frac{\dfrac{1}{\sqrt{2}}}{\dfrac{1}{\sqrt{2}}} = 1\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:5b“