Lösung 4.1:7d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 1: | Zeile 1: | ||
We rewrite the equation in standard form by completing the square for the ''x''- and ''y''-terms, | We rewrite the equation in standard form by completing the square for the ''x''- and ''y''-terms, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
x^{2} - 2x &= (x-1)^2 - 1^2\,,\\[5pt] | x^{2} - 2x &= (x-1)^2 - 1^2\,,\\[5pt] | ||
y^{2} + 2y &= (y+1)^2 - 1^2\,\textrm{.} | y^{2} + 2y &= (y+1)^2 - 1^2\,\textrm{.} | ||
| Zeile 8: | Zeile 8: | ||
Now, the equation is | Now, the equation is | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
(x-1)^2 - 1 + (y+1)^2 - 1 &= -2\\ | (x-1)^2 - 1 + (y+1)^2 - 1 &= -2\\ | ||
\Leftrightarrow\quad (x-1)^2 + (y+1)^2 &= 0\,\textrm{.} | \Leftrightarrow\quad (x-1)^2 + (y+1)^2 &= 0\,\textrm{.} | ||
Version vom 08:49, 22. Okt. 2008
We rewrite the equation in standard form by completing the square for the x- and y-terms,
| \displaystyle \begin{align}
x^{2} - 2x &= (x-1)^2 - 1^2\,,\\[5pt] y^{2} + 2y &= (y+1)^2 - 1^2\,\textrm{.} \end{align} |
Now, the equation is
| \displaystyle \begin{align}
(x-1)^2 - 1 + (y+1)^2 - 1 &= -2\\ \Leftrightarrow\quad (x-1)^2 + (y+1)^2 &= 0\,\textrm{.} \end{align} |
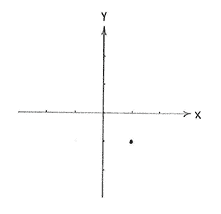
The only point which satisfies this equation is \displaystyle (x,y) = (1,-1) because, for all other values of x and y, the left-hand side is strictly positive and therefore not zero.