Lösung 4.1:10

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 9: Zeile 9:
Because the line is 54 dm long, we have
Because the line is 54 dm long, we have
-
{{Displayed math||<math>y+z=54\,\textrm{.}</math>|(1)}}
+
{{Abgesetzte Formel||<math>y+z=54\,\textrm{.}</math>|(1)}}
Then, the Pythagorean theorem gives the relations
Then, the Pythagorean theorem gives the relations
-
{{Displayed math||<math>y^2 = x^2 + 12^2\,,</math>|(2)}}
+
{{Abgesetzte Formel||<math>y^2 = x^2 + 12^2\,,</math>|(2)}}
-
{{Displayed math||<math>z^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3)}}
+
{{Abgesetzte Formel||<math>z^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3)}}
The idea now is to solve the system of equations (1)-(3) by first eliminating ''z'', so that we get two equations which only contain ''x'' and ''y''. Then, eliminate ''y'' from one of these equations, so that we get an equation which determines ''x''.
The idea now is to solve the system of equations (1)-(3) by first eliminating ''z'', so that we get two equations which only contain ''x'' and ''y''. Then, eliminate ''y'' from one of these equations, so that we get an equation which determines ''x''.
Zeile 20: Zeile 20:
From (1), we have <math>z = 54-y</math>, and substituting this into (3) gives us the equation
From (1), we have <math>z = 54-y</math>, and substituting this into (3) gives us the equation
-
{{Displayed math||<math>(54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3')}}
+
{{Abgesetzte Formel||<math>(54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3')}}
Equations (2) and (3') together give a smaller system for ''x'' and ''y'',
Equations (2) and (3') together give a smaller system for ''x'' and ''y'',
-
{{Displayed math||<math>\left\{ \begin{align}
+
{{Abgesetzte Formel||<math>\left\{ \begin{align}
& y^2 = x^2 + 12^2\,,\\[5pt]
& y^2 = x^2 + 12^2\,,\\[5pt]
& (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}
& (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}
Zeile 31: Zeile 31:
Expand the quadratic terms on both sides of (3'),
Expand the quadratic terms on both sides of (3'),
-
{{Displayed math||<math>54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,</math>}}
+
{{Abgesetzte Formel||<math>54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,</math>}}
and simplify
and simplify
-
{{Displayed math||<math>2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}</math>}}
Use (2) and replace <math>y^2</math> with <math>x^2+12</math> in this equation,
Use (2) and replace <math>y^2</math> with <math>x^2+12</math> in this equation,
-
{{Displayed math||<math>2916 - 108y + x^2 + 144 = x^2 + 12x + 1332</math>}}
+
{{Abgesetzte Formel||<math>2916 - 108y + x^2 + 144 = x^2 + 12x + 1332</math>}}
which gets rid of the ''x''²-term,
which gets rid of the ''x''²-term,
-
{{Displayed math||<math>2916 - 108y + 144 = 12x + 1332\,,</math>}}
+
{{Abgesetzte Formel||<math>2916 - 108y + 144 = 12x + 1332\,,</math>}}
and further simplification gives the equation
and further simplification gives the equation
-
{{Displayed math||<math>12x + 108y = 1728</math>|(3")}}
+
{{Abgesetzte Formel||<math>12x + 108y = 1728</math>|(3")}}
If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and (3"), where one of the equations is linear
If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and (3"), where one of the equations is linear
-
{{Displayed math||<math>\left\{ \begin{align}
+
{{Abgesetzte Formel||<math>\left\{ \begin{align}
& y^2 = x^2 + 12^2\,,\\[5pt]
& y^2 = x^2 + 12^2\,,\\[5pt]
& 12x+108y=1728\,\textrm{.}
& 12x+108y=1728\,\textrm{.}
Zeile 58: Zeile 58:
In this system, we can make ''y'' the subject in (3"),
In this system, we can make ''y'' the subject in (3"),
-
{{Displayed math||<math>y=\frac{1728-12x}{108}=16-\frac{x}{9}</math>}}
+
{{Abgesetzte Formel||<math>y=\frac{1728-12x}{108}=16-\frac{x}{9}</math>}}
and substitute into (2),
and substitute into (2),
-
{{Displayed math||<math>\Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>\Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}</math>}}
This is an equation which only contains ''x'', and if we solve it, we will get our answer.
This is an equation which only contains ''x'', and if we solve it, we will get our answer.
Zeile 68: Zeile 68:
Expand the quadratic on the left-hand side,
Expand the quadratic on the left-hand side,
-
{{Displayed math||<math>16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144</math>}}
+
{{Abgesetzte Formel||<math>16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144</math>}}
and collect together all terms on one side,
and collect together all terms on one side,
-
{{Displayed math||<math>x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,</math>}}
+
{{Abgesetzte Formel||<math>x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,</math>}}
which gives the equation
which gives the equation
-
{{Displayed math||<math>\frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>\frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}</math>}}
Multiply both sides by <math>81/80</math> so that we get the equation in standard form,
Multiply both sides by <math>81/80</math> so that we get the equation in standard form,
-
{{Displayed math||<math>x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}</math>}}
Completing the square on the left-hand side gives
Completing the square on the left-hand side gives
-
{{Displayed math||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0</math>}}
+
{{Abgesetzte Formel||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0</math>}}
and then
and then
-
{{Displayed math||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,</math>}}
+
{{Abgesetzte Formel||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,</math>}}
i.e.
i.e.
-
{{Displayed math||<math>x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}</math>}}
This means that the equation has the solutions
This means that the equation has the solutions
-
{{Displayed math||<math>x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}</math>}}
The answer is thus <math>x=9\ \textrm{dm}</math> (the negative root must be discarded).
The answer is thus <math>x=9\ \textrm{dm}</math> (the negative root must be discarded).
Zeile 105: Zeile 105:
Equation (3") gives
Equation (3") gives
-
{{Displayed math||<math>y = 16-\frac{x}{9} = 16-1 = 15</math>}}
+
{{Abgesetzte Formel||<math>y = 16-\frac{x}{9} = 16-1 = 15</math>}}
and equation (1) gives
and equation (1) gives
-
{{Displayed math||<math>z=54-y=54-15=39\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>z=54-y=54-15=39\,\textrm{.}</math>}}
Now, we check that <math>x=9</math>, <math>y=15</math> and <math>z=39</math> satisfy the equations (1), (2) and (3),
Now, we check that <math>x=9</math>, <math>y=15</math> and <math>z=39</math> satisfy the equations (1), (2) and (3),
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
\textrm{LHS of (1)} &= 15+39 = 54\,,\\[5pt]
\textrm{LHS of (1)} &= 15+39 = 54\,,\\[5pt]
\textrm{RHS of (1)} &= 54\,,\\[10pt]
\textrm{RHS of (1)} &= 54\,,\\[10pt]

Version vom 08:47, 22. Okt. 2008

First, let's decide to determine all distance in dm (decimeters), so that we have all the distances as integers.

Call the length of the washing line from the trees to the hanger y and z, as in the figure below, and introduce two auxiliary triangles which have y and z as their hypotenuses. (As an approximation, we suppose that the taut washing line consists of two straight parts.)


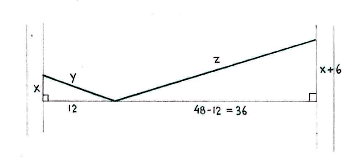
Image:4_1_10-1(5)_.gif


Because the line is 54 dm long, we have

\displaystyle y+z=54\,\textrm{.} (1)

Then, the Pythagorean theorem gives the relations

\displaystyle y^2 = x^2 + 12^2\,, (2)
\displaystyle z^2 = (x+6)^2 + 36^2\,\textrm{.} (3)

The idea now is to solve the system of equations (1)-(3) by first eliminating z, so that we get two equations which only contain x and y. Then, eliminate y from one of these equations, so that we get an equation which determines x.

From (1), we have \displaystyle z = 54-y, and substituting this into (3) gives us the equation

\displaystyle (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} (3')

Equations (2) and (3') together give a smaller system for x and y,

\displaystyle \left\{ \begin{align}

& y^2 = x^2 + 12^2\,,\\[5pt] & (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3')\end{align}

Expand the quadratic terms on both sides of (3'),

\displaystyle 54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,

and simplify

\displaystyle 2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}

Use (2) and replace \displaystyle y^2 with \displaystyle x^2+12 in this equation,

\displaystyle 2916 - 108y + x^2 + 144 = x^2 + 12x + 1332

which gets rid of the x²-term,

\displaystyle 2916 - 108y + 144 = 12x + 1332\,,

and further simplification gives the equation

\displaystyle 12x + 108y = 1728 (3")

If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and (3"), where one of the equations is linear

\displaystyle \left\{ \begin{align}

& y^2 = x^2 + 12^2\,,\\[5pt] & 12x+108y=1728\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3")\end{align}

In this system, we can make y the subject in (3"),

\displaystyle y=\frac{1728-12x}{108}=16-\frac{x}{9}

and substitute into (2),

\displaystyle \Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}

This is an equation which only contains x, and if we solve it, we will get our answer.

Expand the quadratic on the left-hand side,

\displaystyle 16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144

and collect together all terms on one side,

\displaystyle x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,

which gives the equation

\displaystyle \frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}

Multiply both sides by \displaystyle 81/80 so that we get the equation in standard form,

\displaystyle x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}

Completing the square on the left-hand side gives

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0

and then

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,

i.e.

\displaystyle x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}

This means that the equation has the solutions

\displaystyle x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}

The answer is thus \displaystyle x=9\ \textrm{dm} (the negative root must be discarded).


To be sure that we have calculated correctly, we also look at the values of y and z, and check that the original equations (1) to (3) are satisfied.

Equation (3") gives

\displaystyle y = 16-\frac{x}{9} = 16-1 = 15

and equation (1) gives

\displaystyle z=54-y=54-15=39\,\textrm{.}

Now, we check that \displaystyle x=9, \displaystyle y=15 and \displaystyle z=39 satisfy the equations (1), (2) and (3),

\displaystyle \begin{align}

\textrm{LHS of (1)} &= 15+39 = 54\,,\\[5pt] \textrm{RHS of (1)} &= 54\,,\\[10pt] \textrm{LHS of (2)} &= 15^2 = 225\,,\\[5pt] \textrm{RHS of (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt] \textrm{LHS of (3)} &= 39^2 = 1521\,,\\[5pt] \textrm{RHS of (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:10“