Lösung 2.2:5c
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 2: | Zeile 2: | ||
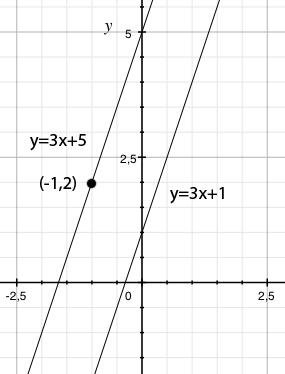
<math>y=3x+1</math>, we can read off that it has a slope of 3 (the coefficient in front of ''x''), and hence the equation we are looking for has an equation of the form | <math>y=3x+1</math>, we can read off that it has a slope of 3 (the coefficient in front of ''x''), and hence the equation we are looking for has an equation of the form | ||
| - | {{ | + | {{Abgesetzte Formel||<math>y=3x+m\,,</math>}} |
where ''m'' is a constant. The condition that the line should also contain the point (-1,2) means that the point should satisfy the equation of the line | where ''m'' is a constant. The condition that the line should also contain the point (-1,2) means that the point should satisfy the equation of the line | ||
| - | {{ | + | {{Abgesetzte Formel||<math>2=3\cdot (-1)+m\,,</math>}} |
which gives <math>m=5</math>. Hence, the equation of the line is <math>y=3x+5</math>. | which gives <math>m=5</math>. Hence, the equation of the line is <math>y=3x+5</math>. | ||
Version vom 08:28, 22. Okt. 2008
Two straight lines are parallel if they have the same slope. From the line \displaystyle y=3x+1, we can read off that it has a slope of 3 (the coefficient in front of x), and hence the equation we are looking for has an equation of the form
| \displaystyle y=3x+m\,, |
where m is a constant. The condition that the line should also contain the point (-1,2) means that the point should satisfy the equation of the line
| \displaystyle 2=3\cdot (-1)+m\,, |
which gives \displaystyle m=5. Hence, the equation of the line is \displaystyle y=3x+5.