Lösung 4.4:5b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
Let's first investigate when the equality | Let's first investigate when the equality | ||
| + | {{Displayed math||<math>\tan u=\tan v</math>}} | ||
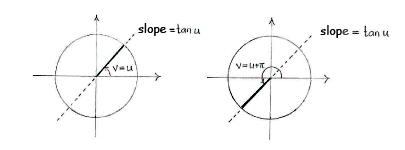
| - | + | is satisfied. Because <math>\tan u</math> can be interpreted as the slope (gradient) of the line which makes an angle ''u'' with the positive ''x''-axis, we see that for a fixed value of <math>\tan u</math>, there are two angles ''v'' in the unit circle with this slope, | |
| - | + | ||
| - | + | ||
| - | is satisfied. Because | + | |
| - | <math>u</math> | + | |
| - | can be interpreted as the slope (gradient) of the line which makes an angle | + | |
| - | + | ||
| - | with the positive | + | |
| - | + | ||
| - | -axis, we see that for a fixed value of tan u, there are two angles | + | |
| - | + | ||
| - | in the unit circle with this slope | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>v=u\qquad\text{and}\qquad v=u+\pi\,\textrm{.}</math>}} | ||
[[Image:4_4_5_b.gif|center]] | [[Image:4_4_5_b.gif|center]] | ||
| - | slope | + | The angle ''v'' has the same slope after every half turn, so if we add multiples of |
| - | <math> | + | <math>\pi</math> to ''u'', we will obtain all the angles ''v'' which satisfy the equality |
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>v=u+n\pi\,,</math>}} | ||
| - | + | where ''n'' is an arbitrary integer. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | where | + | |
| - | + | ||
| - | is an arbitrary integer. | + | |
If we apply this result to the equation | If we apply this result to the equation | ||
| - | + | {{Displayed math||<math>\tan x=\tan 4x</math>}} | |
| - | <math>\tan x=\tan 4x</math> | + | |
| - | + | ||
we see that the solutions are given by | we see that the solutions are given by | ||
| + | {{Displayed math||<math>4x = x+n\pi\qquad\text{(n is an arbitrary integer),}</math>}} | ||
| - | + | and solving for ''x'' gives | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | and solving for | + | |
| - | + | ||
| - | gives | + | |
| - | + | ||
| - | <math>x=\ | + | {{Displayed math||<math>x = \tfrac{1}{3}n\pi\qquad\text{(n is an arbitrary integer).}</math>}} |
| - | ( | + | |
| - | + | ||
| - | an arbitrary integer). | + | |
Version vom 14:02, 13. Okt. 2008
Let's first investigate when the equality
is satisfied. Because \displaystyle \tan u can be interpreted as the slope (gradient) of the line which makes an angle u with the positive x-axis, we see that for a fixed value of \displaystyle \tan u, there are two angles v in the unit circle with this slope,
The angle v has the same slope after every half turn, so if we add multiples of \displaystyle \pi to u, we will obtain all the angles v which satisfy the equality
where n is an arbitrary integer.
If we apply this result to the equation
we see that the solutions are given by
and solving for x gives