Lösung 4.2:2a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
The opposite and adjacent are given in the right-angled triangle and this means that the value of the tangent for the angle can be determined as the quotient between the opposite and the adjacent:
The opposite and adjacent are given in the right-angled triangle and this means that the value of the tangent for the angle can be determined as the quotient between the opposite and the adjacent:
 +
{| width="100%"
 +
| width="50%" align="center"|<math>\tan v = 2/5</math>
 +
| width="50%" align="left"|[[Image:4_2_2_a.gif]]
 +
|}
-
<math>\text{tan }v\text{ }={2}/{5}\;~</math>
+
At the same time, this is a trigonometric equation for the angle ''v''.
-
[[Image:4_2_2_a.gif|center]]
+
Note: In the chapter on "Trigonometric equations", we will investigate more closely how to solve equations of this type.
-
 
+
-
At the same time, this is a trigonometric equation for the angle
+
-
<math>v</math>.
+
-
 
+
-
NOTE: In the chapter on "Trigonometric equations", we will investigate more closely how to solve equations of this type.
+

Version vom 12:16, 10. Okt. 2008

The opposite and adjacent are given in the right-angled triangle and this means that the value of the tangent for the angle can be determined as the quotient between the opposite and the adjacent:

\displaystyle \tan v = 2/5 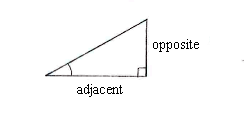Image:4_2_2_a.gif

At the same time, this is a trigonometric equation for the angle v.


Note: In the chapter on "Trigonometric equations", we will investigate more closely how to solve equations of this type.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:2a“