Lösung 4.3:5

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
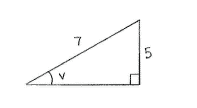
An often-used technique to calculate
+
An often-used technique to calculate <math>\cos v</math> and <math>\tan v</math>, given the sine value of an acute angle, is to draw the angle <math>v</math> in a right-angled triangle which has two sides arranged so that <math>\sin v = 5/7\,</math>.
-
<math>\text{cos }v</math>
+
-
and
+
-
<math>\text{tan }v</math>, given the sine value of an acute angle, is to draw the angle
+
-
<math>v</math>
+
-
in a right-angled triangle which has two sides arranged so that
+
-
<math>\text{sin }v={5}/{7}\;</math>.
+
-
 
+
-
 
+
[[Image:4_3_5_1.gif|center]]
[[Image:4_3_5_1.gif|center]]
-
Using Pythagoras' theorem, we can determine the length of the third side in the triangle.
+
Using the Pythagorean theorem, we can determine the length of the third side in the triangle.
-
 
+
{| align="center"
-
[[Image:4_3_5_2.gif|center]]
+
||[[Image:4_3_5_2.gif]]
-
 
+
||<math>\begin{align}&x^2 + 5^2 = 7^2\\[5pt] &\text{which gives that}\\[5pt] &x = \sqrt{7^2-5^2} = \sqrt{24} = 2\sqrt{6}\end{align}</math>
-
 
+
|}
-
<math>x^{2}+5^{2}=7^{2}</math>
+
-
which gives that
+
-
<math>x=\sqrt{7^{2}-5^{2}}=\sqrt{24}=2\sqrt{6}</math>
+
Then, using the definition of cosine and tangent,
Then, using the definition of cosine and tangent,
-
 
+
{{Displayed math||<math>\begin{align}
-
<math>\begin{align}
+
\cos v &= \frac{x}{7} = \frac{2\sqrt{6}}{7}\,,\\[5pt]
-
& \cos v=\frac{x}{7}=\frac{2\sqrt{6}}{7}, \\
+
\tan v &= \frac{5}{x} = \frac{5}{2\sqrt{6}}\,\textrm{.}
-
& \tan v=\frac{5}{x}=\frac{5}{2\sqrt{6}} \\
+
\end{align}</math>}}
-
\end{align}</math>
+
-
NOTE: Note that the right-angled triangle that we use is just a tool and has nothing to do with the triangle that is referred to in the question.
+
Note: The right-angled triangle that we use is just a tool and has nothing to do with the triangle that is referred to in the question.

Version vom 14:33, 9. Okt. 2008

An often-used technique to calculate \displaystyle \cos v and \displaystyle \tan v, given the sine value of an acute angle, is to draw the angle \displaystyle v in a right-angled triangle which has two sides arranged so that \displaystyle \sin v = 5/7\,.

Using the Pythagorean theorem, we can determine the length of the third side in the triangle.

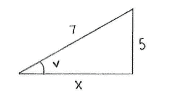
Image:4_3_5_2.gif \displaystyle \begin{align}&x^2 + 5^2 = 7^2\\[5pt] &\text{which gives that}\\[5pt] &x = \sqrt{7^2-5^2} = \sqrt{24} = 2\sqrt{6}\end{align}

Then, using the definition of cosine and tangent,

Vorlage:Displayed math


Note: The right-angled triangle that we use is just a tool and has nothing to do with the triangle that is referred to in the question.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.3:5“