Lösung 4.3:1a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
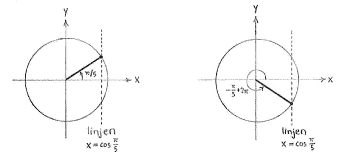
If we draw the angle
+
If we draw the angle <math>\pi/5</math> on the unit circle, then it will have an ''x''-coordinate that is equal to <math>\cos \pi/5\,</math>.
-
<math>{\pi }/{5}\;</math>
+
-
on a unit circle, then it will have an
+
-
<math>x</math>
+
-
-coordinate that is equal to
+
-
<math>{\cos \pi }/{5}\;</math>
+
 +
[[Image:4_3_1_a.gif||center]]
-
<center> [[Image:4_3_1_a.gif]] </center>
+
In the figures, we see also that the only other angle between <math>0</math> and <math>2\pi</math> which has the same cosine value, i.e. same ''x''-coordinate, is the angle <math>v=-\pi/5+2\pi = 9\pi/5</math> on the opposite side of the ''x''-axis.
-
 
+
-
the line
+
-
<math>x={\cos \pi }/{5}\;</math
+
-
 
+
-
 
+
-
 
+
-
In the figures, we see also that the only other angle between
+
-
<math>0</math>
+
-
and
+
-
<math>2\pi </math>
+
-
which has the same cosine value, i.e. same
+
-
<math>x</math>
+
-
-coordinate, is the angle
+
-
<math>v=-\frac{\pi }{5}+2\pi =\frac{9\pi }{5}</math>
+
-
on the opposite side of the
+
-
<math>x</math>
+
-
-axis.
+

Version vom 12:57, 9. Okt. 2008

If we draw the angle \displaystyle \pi/5 on the unit circle, then it will have an x-coordinate that is equal to \displaystyle \cos \pi/5\,.

In the figures, we see also that the only other angle between \displaystyle 0 and \displaystyle 2\pi which has the same cosine value, i.e. same x-coordinate, is the angle \displaystyle v=-\pi/5+2\pi = 9\pi/5 on the opposite side of the x-axis.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.3:1a“