Lösung 4.2:4b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
We start by subtracting
+
We start by subtracting <math>2\pi</math> from <math>11\pi/3</math>, so that we get an angle between <math>0</math> and <math>2\pi </math>. This doesn't change the cosine value
-
<math>2\pi </math>
+
-
from
+
-
<math>\frac{11\pi }{3}</math>, so that we get an angle between
+
-
<math>o</math>
+
-
and
+
-
<math>2\pi </math>. This doesn't change the cosine value
+
 +
{{Displayed math||<math>\cos\frac{11\pi}{3} = \cos\Bigl(\frac{11\pi}{3}-2\pi\Bigr) = \cos\frac{5\pi}{3}\,\textrm{.}</math>}}
-
<math>\cos \frac{11\pi }{3}=\cos \left( \frac{11\pi }{3}-2\pi \right)=\cos \frac{5\pi }{3}</math>
+
Then, by rewriting <math>5\pi/3</math> as a sum of <math>\pi</math>- and <math>\pi/2</math>-terms,
 +
{{Displayed math||<math>\frac{5\pi}{3} = \frac{3\pi +\dfrac{3}{2}\pi +\dfrac{1}{2}\pi}{3} = \pi + \frac{\pi}{2} + \frac{\pi}{6}</math>}}
-
Then, by rewriting
+
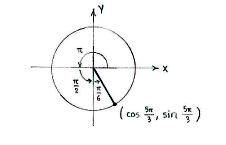
we see that <math>5\pi/3</math> is an angle in the fourth quadrant which makes an angle <math>\pi/6</math> with the negative ''y''-axis.
-
<math>\frac{5\pi }{3}</math>
+
-
as a sum of
+
-
<math>\pi </math>
+
-
- and
+
-
<math>\frac{\pi }{2}</math>
+
-
-terms
+
 +
[[Image:4_2_4b1.gif||center]]
-
<math>\frac{5\pi }{3}=\frac{3\pi +\frac{3}{2}\pi +\frac{1}{2}\pi }{3}=\pi +\frac{\pi }{2}+\frac{\pi }{6}</math>
+
With the help of an auxiliary triangle and a little trigonometry, we can determine the coordinates for the point on a unit circle which corresponds to the angle
 +
<math>5\pi/3\,</math>.
-
we see that
+
{| width="100%"
-
<math>\frac{5\pi }{3}</math>
+
|width="50%" align="center"|[[Image:4_2_4_b2.gif]]
-
is an angle in the fourth quadrant which makes an angle
+
|width="50%" align="left"|<math>\begin{align}\text{opposite} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{adjacent} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align}</math>
-
<math>\frac{\pi }{6}</math>
+
|}
-
with the negative
+
-
<math>y</math>
+
-
-axis.
+
 +
The point has coordinates <math>(1/2,-\sqrt{3}/2)</math> and
-
[[Image:4_2_4b1.gif]]
+
{{Displayed math||<math>\cos \frac{11\pi}{3} = \cos\frac{5\pi}{3} = \frac{1}{2}\,\textrm{.}</math>}}
-
 
+
-
With the help of a triangle and a little trigonometry, we can determine the coordinates for the point on a unit circle which corresponds to the angle
+
-
<math>\frac{5\pi }{3}</math> .
+
-
 
+
-
 
+
-
[[Image:4_2_4_b2.gif]]
+
-
 
+
-
The point has coordinates
+
-
<math>\left( \frac{1}{2} \right.,\left. -\frac{\sqrt{3}}{2} \right)</math>
+
-
and
+
-
<math>\cos \frac{11\pi }{3}=\cos \frac{5\pi }{3}=\frac{1}{2}</math>.
+

Version vom 08:37, 9. Okt. 2008

We start by subtracting \displaystyle 2\pi from \displaystyle 11\pi/3, so that we get an angle between \displaystyle 0 and \displaystyle 2\pi . This doesn't change the cosine value

Vorlage:Displayed math

Then, by rewriting \displaystyle 5\pi/3 as a sum of \displaystyle \pi- and \displaystyle \pi/2-terms,

Vorlage:Displayed math

we see that \displaystyle 5\pi/3 is an angle in the fourth quadrant which makes an angle \displaystyle \pi/6 with the negative y-axis.

With the help of an auxiliary triangle and a little trigonometry, we can determine the coordinates for the point on a unit circle which corresponds to the angle \displaystyle 5\pi/3\,.

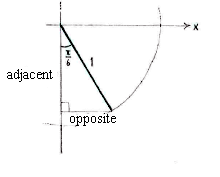
Image:4_2_4_b2.gif \displaystyle \begin{align}\text{opposite} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{adjacent} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align}

The point has coordinates \displaystyle (1/2,-\sqrt{3}/2) and

Vorlage:Displayed math

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:4b“