Aus Online Mathematik Brückenkurs 1

Version vom 10:27, 28. Sep. 2008 (bearbeiten) Ian (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 13:52, 8. Okt. 2008 (bearbeiten) (rückgängig) Tek (Diskussion | Beiträge) K Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
-	[[Image:4_2_1_a.gif|center]]
-
-
-
	The definition of the tangent states that		The definition of the tangent states that
-		+	{| width="100%"
-		+	| width="50%" align="center"|<math>\tan u=\frac{\text{opposite}}{\text{adjacent}}</math>
-	<math>\tan u=\frac{\text{opposite}}{\text{adjacent}}</math>	+	| width="50%" align="center"|[[Image:4_2_1_a.gif]]
-		+	|}
	In our case, this means that		In our case, this means that
		+	{{Displayed math||<math>\tan 27^{\circ} = \frac{x}{13}</math>}}
-	<math>\tan 27^{\circ }=\frac{x}{13}</math>	+	which gives <math>x = 13\cdot \tan 27^{\circ}\,</math>.
-		+
-		+
-	which gives	+
-	<math>x=\text{13}\centerdot \text{tan 27}^{\circ }</math>.	+
-	NOTE: Using a calculator, we can work out what
-	<math>x\text{ }</math>
-	should be:
		+	Note: Using a calculator, we can work out what ''x'' should be,
-	<math>x=\text{13}\centerdot \text{tan 27}^{\circ }\approx 6.62</math>	+	{{Displayed math||<math>x = 13\cdot\tan 27^{\circ} \approx 6\textrm{.}62\,\textrm{.}</math>}}

---

Version vom 13:52, 8. Okt. 2008

The definition of the tangent states that

\displaystyle \tan u=\frac{\text{opposite}}{\text{adjacent}}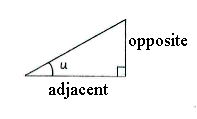

In our case, this means that

Vorlage:Displayed math

which gives \displaystyle x = 13\cdot \tan 27^{\circ}\,.

Note: Using a calculator, we can work out what x should be,

Vorlage:Displayed math