Lösung 4.4:5b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.4:5b moved to Solution 4.4:5b: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Let's first investigate when the equality
-
<center> [[Image:4_4_5b-1(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
 
-
{{NAVCONTENT_START}}
+
<math>\tan u=\tan v</math>
-
<center> [[Image:4_4_5b-2(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
 
 +
is satisfied. Because
 +
<math>u</math>
 +
can be interpreted as the slope (gradient) of the line which makes an angle
 +
<math>u</math>
 +
with the positive
 +
<math>x</math>
 +
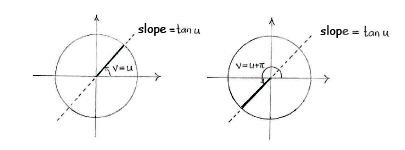
-axis, we see that for a fixed value of tan u, there are two angles
 +
<math>v</math>
 +
in the unit circle with this slope:
 +
 
 +
 
 +
<math>v=u</math>
 +
and
 +
<math>v=u+\pi </math>
 +
 
[[Image:4_4_5_b.gif|center]]
[[Image:4_4_5_b.gif|center]]
 +
 +
slope
 +
<math>=\text{ tan }u</math>
 +
slope
 +
<math>=\text{ tan }u</math>
 +
 +
 +
The angle
 +
<math>v</math>
 +
has the same slope after every half turn, so if we add multiples of
 +
<math>\pi \text{ }</math>
 +
to
 +
<math>u</math>, we will obtain all the angles
 +
<math>v</math>
 +
which satisfy the equality
 +
 +
 +
<math>v=u+n\pi </math>
 +
 +
 +
where
 +
<math>n</math>
 +
is an arbitrary integer.
 +
 +
If we apply this result to the equation
 +
 +
 +
<math>\tan x=\tan 4x</math>
 +
 +
 +
we see that the solutions are given by
 +
 +
 +
<math>4x=x+n\pi </math>
 +
(
 +
<math>n</math>
 +
an arbitrary integer),
 +
 +
and solving for
 +
<math>x</math>
 +
gives
 +
 +
 +
<math>x=\frac{1}{3}n\pi </math>
 +
(
 +
<math>n</math>
 +
an arbitrary integer).

Version vom 11:06, 1. Okt. 2008

Let's first investigate when the equality


\displaystyle \tan u=\tan v


is satisfied. Because \displaystyle u can be interpreted as the slope (gradient) of the line which makes an angle \displaystyle u with the positive \displaystyle x -axis, we see that for a fixed value of tan u, there are two angles \displaystyle v in the unit circle with this slope:


\displaystyle v=u and \displaystyle v=u+\pi


slope \displaystyle =\text{ tan }u slope \displaystyle =\text{ tan }u


The angle \displaystyle v has the same slope after every half turn, so if we add multiples of \displaystyle \pi \text{ } to \displaystyle u, we will obtain all the angles \displaystyle v which satisfy the equality


\displaystyle v=u+n\pi


where \displaystyle n is an arbitrary integer.

If we apply this result to the equation


\displaystyle \tan x=\tan 4x


we see that the solutions are given by


\displaystyle 4x=x+n\pi ( \displaystyle n an arbitrary integer),

and solving for \displaystyle x gives


\displaystyle x=\frac{1}{3}n\pi ( \displaystyle n an arbitrary integer).

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:5b“