Lösung 4.4:2c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.4:2c moved to Solution 4.4:2c: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
There are two angles in the unit circle,
-
<center> [[Image:4_4_2c.gif]] </center>
+
<math>x=0\text{ }</math>
-
{{NAVCONTENT_STOP}}
+
and
 +
<math>x=\pi </math>, whose sine has a value of zero.
[[Image:4_4_2_c.gif|center]]
[[Image:4_4_2_c.gif|center]]
 +
 +
We get the full solution when we add multiples of
 +
<math>2\pi </math>,
 +
 +
 +
<math>x=0+2n\pi </math>
 +
and
 +
<math>x=\pi +2n\pi </math>,
 +
 +
where
 +
<math>n</math>
 +
is an arbitrary integer.
 +
 +
NOTE: Because the difference between
 +
<math>0</math>
 +
and
 +
<math>\pi </math>
 +
is a half turn, the solutions are repeated every half turn and they can be summarized in one expression:
 +
 +
 +
<math>x=0+n\pi </math>
 +
 +
 +
where
 +
<math>n</math>
 +
is an arbitrary integer.

Version vom 13:47, 30. Sep. 2008

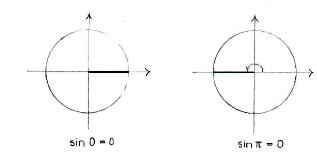
There are two angles in the unit circle, \displaystyle x=0\text{ } and \displaystyle x=\pi , whose sine has a value of zero.

We get the full solution when we add multiples of \displaystyle 2\pi ,


\displaystyle x=0+2n\pi and \displaystyle x=\pi +2n\pi ,

where \displaystyle n is an arbitrary integer.

NOTE: Because the difference between \displaystyle 0 and \displaystyle \pi is a half turn, the solutions are repeated every half turn and they can be summarized in one expression:


\displaystyle x=0+n\pi


where \displaystyle n is an arbitrary integer.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:2c“