Lösung 4.3:9
Aus Online Mathematik Brückenkurs 1
K (Lösning 4.3:9 moved to Solution 4.3:9: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | {{ | + | Using the formula for double angles on sin |
| - | < | + | <math>160^{\circ }</math> |
| - | {{ | + | gives |
| - | {{ | + | |
| - | < | + | |
| - | {{ | + | <math>\sin 160^{\circ }=2\cos 80^{\circ }\sin 80^{\circ }</math> |
| + | |||
| + | |||
| + | On the right-hand side, we see that the factor | ||
| + | <math>\cos 80^{\circ }</math> | ||
| + | has appeared, and if we use the formula for double angles on the second factor ( | ||
| + | <math>\sin 80^{\circ }</math> | ||
| + | ), | ||
| + | |||
| + | |||
| + | <math>2\cos 80^{\circ }\sin 80^{\circ }=2\cos 80^{\circ }\centerdot 2\cos 40^{\circ }\sin 40^{\circ }</math> | ||
| + | |||
| + | |||
| + | we obtain a further factor | ||
| + | <math>\cos 40^{\circ }</math>. A final application of the formula for double angles on | ||
| + | <math>\sin 40^{\circ }</math> | ||
| + | gives us all three cosine factors: | ||
| + | |||
| + | |||
| + | <math>2\cos 80^{\circ }\centerdot 2\cos 40^{\circ }\centerdot \sin 40^{\circ }=2\cos 80^{\circ }\centerdot 2\cos 40^{\circ }\centerdot 2\cos 20^{\circ }\sin 20^{\circ }</math> | ||
| + | |||
| + | |||
| + | We have thus succeeded in showing that | ||
| + | |||
| + | |||
| + | <math>\sin 160^{\circ }=8\cos 80^{\circ }\centerdot \cos 40^{\circ }\centerdot \cos 20^{\circ }\sin 20^{\circ }</math> | ||
| + | |||
| + | |||
| + | which can also be written as | ||
| + | |||
| + | |||
| + | <math>\cos 80^{\circ }\centerdot \cos 40^{\circ }\centerdot \cos 20^{\circ }=\frac{\sin 160^{\circ }}{8\sin 20^{\circ }}</math> | ||
| + | |||
| + | |||
| + | If we draw the unit circle, we see that | ||
| + | <math>160^{\circ }</math> | ||
| + | makes an angle of | ||
| + | <math>20^{\circ }</math> | ||
| + | with the negative | ||
| + | <math>x</math> | ||
| + | -axis, and therefore the angles | ||
| + | <math>20^{\circ }</math> | ||
| + | and | ||
| + | <math>160^{\circ }</math> | ||
| + | have the same | ||
| + | <math>y</math> | ||
| + | -coordinate in the unit circle, i.e. | ||
| + | |||
| + | <math>\sin 20^{\circ }=\sin 160^{\circ }</math>. | ||
| + | |||
[[Image:4_3_9.gif|center]] | [[Image:4_3_9.gif|center]] | ||
| + | |||
| + | This shows that | ||
| + | |||
| + | |||
| + | <math>\cos 80^{\circ }\centerdot \cos 40^{\circ }\centerdot \cos 20^{\circ }=\frac{\sin 160^{\circ }}{8\sin 20^{\circ }}=\frac{1}{8}</math> | ||
Version vom 11:31, 30. Sep. 2008
Using the formula for double angles on sin \displaystyle 160^{\circ } gives
\displaystyle \sin 160^{\circ }=2\cos 80^{\circ }\sin 80^{\circ }
On the right-hand side, we see that the factor
\displaystyle \cos 80^{\circ }
has appeared, and if we use the formula for double angles on the second factor (
\displaystyle \sin 80^{\circ }
),
\displaystyle 2\cos 80^{\circ }\sin 80^{\circ }=2\cos 80^{\circ }\centerdot 2\cos 40^{\circ }\sin 40^{\circ }
we obtain a further factor
\displaystyle \cos 40^{\circ }. A final application of the formula for double angles on
\displaystyle \sin 40^{\circ }
gives us all three cosine factors:
\displaystyle 2\cos 80^{\circ }\centerdot 2\cos 40^{\circ }\centerdot \sin 40^{\circ }=2\cos 80^{\circ }\centerdot 2\cos 40^{\circ }\centerdot 2\cos 20^{\circ }\sin 20^{\circ }
We have thus succeeded in showing that
\displaystyle \sin 160^{\circ }=8\cos 80^{\circ }\centerdot \cos 40^{\circ }\centerdot \cos 20^{\circ }\sin 20^{\circ }
which can also be written as
\displaystyle \cos 80^{\circ }\centerdot \cos 40^{\circ }\centerdot \cos 20^{\circ }=\frac{\sin 160^{\circ }}{8\sin 20^{\circ }}
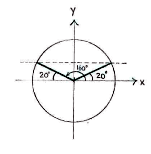
If we draw the unit circle, we see that
\displaystyle 160^{\circ }
makes an angle of
\displaystyle 20^{\circ }
with the negative
\displaystyle x
-axis, and therefore the angles
\displaystyle 20^{\circ }
and
\displaystyle 160^{\circ }
have the same
\displaystyle y
-coordinate in the unit circle, i.e.
\displaystyle \sin 20^{\circ }=\sin 160^{\circ }.
This shows that
\displaystyle \cos 80^{\circ }\centerdot \cos 40^{\circ }\centerdot \cos 20^{\circ }=\frac{\sin 160^{\circ }}{8\sin 20^{\circ }}=\frac{1}{8}