Lösung 2.3:10d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | We can rewrite the double inequality | + | We can rewrite the double inequality <math>x^2\le y\le x</math> as <math>x^2\le y</math> and <math>y\le x\,</math>. These two inequalities define the region above the parabola <math>y=x^2</math> and the region below the line <math>y=x</math>. |
| - | [[Image:2_3_10_d1.gif|center]] | + | |
| + | |||
| + | {| align="center" | ||
| + | |align="center"|[[Image:2_3_10_d1-1.gif|center]] | ||
| + | |width="10px"| | ||
| + | |align="center"|[[Image:2_3_10_d1-2.gif|center]] | ||
| + | |- | ||
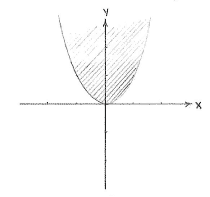
| + | |align="center"|<small>The region ''x''² ≤ ''y''</small> | ||
| + | || | ||
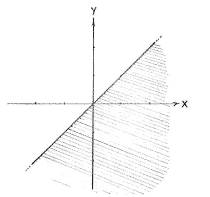
| + | |align="center"|<small>The region ''y'' ≤ ''x''</small> | ||
| + | |} | ||
| + | |||
| + | |||
The region which the inequalities both define is the region in the first quadrant that is bordered below by the parabola and above by the line. | The region which the inequalities both define is the region in the first quadrant that is bordered below by the parabola and above by the line. | ||
| - | [[Image:2_3_10_d2.gif|center]] | + | |
| + | |||
| + | {| align="center" | ||
| + | |align="center"|[[Image:2_3_10_d2.gif|center]] | ||
| + | |- | ||
| + | |align="center"|<small>The region ''x''² ≤ y ≤ x</small> | ||
| + | |} | ||
Version vom 07:30, 30. Sep. 2008
We can rewrite the double inequality \displaystyle x^2\le y\le x as \displaystyle x^2\le y and \displaystyle y\le x\,. These two inequalities define the region above the parabola \displaystyle y=x^2 and the region below the line \displaystyle y=x.
| The region x² ≤ y | The region y ≤ x |
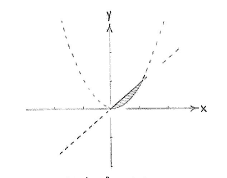
The region which the inequalities both define is the region in the first quadrant that is bordered below by the parabola and above by the line.
| The region x² ≤ y ≤ x |