Lösung 2.3:9c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
To determine all the points on the curve
+
To determine all the points on the curve <math>y=3x^{2}-12x+9</math> which also lie on the ''x''-axis we substitute the equation of the ''x''-axis i.e. <math>y=0</math> in the equation of the curve and obtain that ''x'' must satisfy
-
<math>y=3x^{2}-12x+9</math>
+
-
which also lie on the
+
-
<math>x</math>
+
-
-axis we substitute the equation of the
+
-
<math>x</math>
+
-
-axis i.e.
+
-
<math>y=0</math>
+
-
in the equation of the curve and obtain that
+
-
<math>x</math>
+
-
must satisfy
+
 +
{{Displayed math||<math>0 = 3x^{2}-12x+9\,\textrm{.}</math>}}
-
<math>3x^{2}-12x+9=0</math>
+
After dividing by 3 and completing the square the right-hand side is
 +
{{Displayed math||<math>x^{2}-4x+3 = (x-2)^{2} - 2^{2} + 3 = (x-2)^{2} - 1</math>}}
-
After dividing by
+
and thus the equation has solutions <math>x=2\pm 1,</math>
-
<math>3</math>
+
i.e. <math>x=2-1=1</math> and <math>x=2+1=3\,</math>.
-
and completing the square the right-hand side is
+
-
 
+
-
 
+
-
<math>x^{2}-4x+3=\left( x-2 \right)^{2}-2^{2}+3=\left( x-2 \right)^{2}-1</math>
+
-
 
+
-
 
+
-
and thus the equation has solutions
+
-
 
+
-
 
+
-
<math>x=2\pm 1,</math>
+
-
i.e.
+
-
<math>x=2-1=1</math>
+
-
and
+
-
<math>x=2+1=3.</math>
+
-
 
+
-
 
+
-
The points where the curve cut the
+
-
<math>x</math>
+
-
-axis are
+
-
 
+
-
 
+
-
<math>\left( 1 \right.,\left. 0 \right)</math>
+
-
and
+
-
<math>\left( 3 \right.,\left. 0 \right)</math>
+
 +
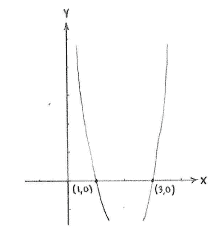
The points where the curve cut the ''x''-axis are (1,0) and (3,0).
[[Image:2_3_9_c.gif|center]]
[[Image:2_3_9_c.gif|center]]

Version vom 14:16, 29. Sep. 2008

To determine all the points on the curve \displaystyle y=3x^{2}-12x+9 which also lie on the x-axis we substitute the equation of the x-axis i.e. \displaystyle y=0 in the equation of the curve and obtain that x must satisfy

Vorlage:Displayed math

After dividing by 3 and completing the square the right-hand side is

Vorlage:Displayed math

and thus the equation has solutions \displaystyle x=2\pm 1, i.e. \displaystyle x=2-1=1 and \displaystyle x=2+1=3\,.

The points where the curve cut the x-axis are (1,0) and (3,0).


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.3:9c“