Lösung 2.3:9a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
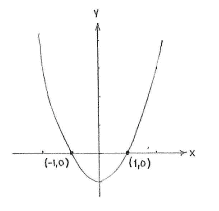
| - | A point lies on the | + | A point lies on the ''x''-axis if it has ''y''-coordinate 0 and we therefore look for all the points on the curve <math>y=x^{2}-1</math> where <math>y=0</math>, i.e. all points which satisfy the equation |
| - | + | ||
| - | -axis if it has | + | |
| - | + | ||
| - | -coordinate | + | |
| - | + | ||
| - | and we therefore look for all the points on the curve | + | |
| - | <math>y=x^ | + | |
| - | where | + | |
| - | <math>y=0</math>, i.e. all points which satisfy the equation | + | |
| + | {{Displayed math||<math>0=x^{2}-1\,\textrm{.}</math>}} | ||
| - | + | This equation has solutions <math>x=\pm 1</math>, which means that the points of intersection are <math>(-1,0)</math> and <math>(1,0)</math>. | |
| - | + | ||
| - | + | ||
| - | This equation has solutions | + | |
| - | <math>x=\pm | + | |
| - | <math> | + | |
| - | and | + | |
| - | <math> | + | |
[[Image:2_3_9_a.gif|center]] | [[Image:2_3_9_a.gif|center]] | ||
Version vom 13:14, 29. Sep. 2008
A point lies on the x-axis if it has y-coordinate 0 and we therefore look for all the points on the curve \displaystyle y=x^{2}-1 where \displaystyle y=0, i.e. all points which satisfy the equation
This equation has solutions \displaystyle x=\pm 1, which means that the points of intersection are \displaystyle (-1,0) and \displaystyle (1,0).