Aus Online Mathematik Brückenkurs 1

Version vom 10:51, 21. Sep. 2008 (bearbeiten) Ian (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 11:29, 29. Sep. 2008 (bearbeiten) (rückgängig) Tek (Diskussion | Beiträge) K Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
-	Using the squaring rule, we recognize the polynomial as the expansion of	+	Using the rule <math>(a+b)^2=a^2+2ab+b^2</math>, we recognize the polynomial as the expansion of <math>(x-1)^{2}\,</math>,
-	<math>\left( x-1 \right)^{2}</math>,	+
		+	{{Displayed math||<math>x^{2}-2x+1 = (x-1)^{2}\,\textrm{.}</math>}}
-	<math>x^{2}-2x+1=\left( x-1 \right)^{2}</math>	+	This quadratic expression has its smallest value, zero, when <math>x-1=0</math>, i.e.
		+	<math>x=1</math>. All non-zero values of <math>x-1</math> give a positive value for
		+	<math>(x-1)^{2}</math>.
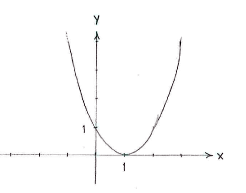
-	This quadratic expression has its smallest value, zero, when	+	Note: If we draw the curve <math>y=(x-1)^{2}</math>, we see that it has a minimum value of zero at <math>x=1\,</math>.
-	<math>x-\text{1}=0</math>, i.e.	+
-	<math>x=\text{1}</math>. All non-zero values of	+
-	<math>x-\text{1}</math>	+
-	give a positive value for	+
-	<math>\left( x-1 \right)^{2}</math>.	+
-		+
-	NOTE: If we draw the curve	+
-	<math>y=\left( x-1 \right)^{2}</math>, we see that it has a minimum value of zero at	+
-	<math>x=\text{1}</math>.	+
	[[Image:2_3_6_a.gif|center]]		[[Image:2_3_6_a.gif|center]]

---

Version vom 11:29, 29. Sep. 2008

Using the rule \displaystyle (a+b)^2=a^2+2ab+b^2, we recognize the polynomial as the expansion of \displaystyle (x-1)^{2}\,,

Vorlage:Displayed math

This quadratic expression has its smallest value, zero, when \displaystyle x-1=0, i.e. \displaystyle x=1. All non-zero values of \displaystyle x-1 give a positive value for \displaystyle (x-1)^{2}.

Note: If we draw the curve \displaystyle y=(x-1)^{2}, we see that it has a minimum value of zero at \displaystyle x=1\,.