Lösung 4.3:1b
Aus Online Mathematik Brückenkurs 1
| Zeile 12: | Zeile 12: | ||
| - | + | <center> [[Image:4_3_1_b.gif]] </center> | |
| - | + | ||
| + | the line | ||
<math>{y=\sin \pi }/{7}\;</math> | <math>{y=\sin \pi }/{7}\;</math> | ||
| - | + | the line | |
<math>{y=\sin \pi }/{7}\;</math> | <math>{y=\sin \pi }/{7}\;</math> | ||
Version vom 10:14, 29. Sep. 2008
Because the sine value for an angle is equal to the angle's \displaystyle y -coordinate on a unit circle, two angles have the same sine value only if they have the same \displaystyle y-coordinate. Therefore, if we draw in the angle \displaystyle {\pi }/{7}\; on a unit circle, we see that the only angle between \displaystyle {\pi }/{2}\; and \displaystyle \pi which has the same sine value lies in the second quadrant, where the line \displaystyle {y=\sin \pi }/{7}\; cuts the unit circle.
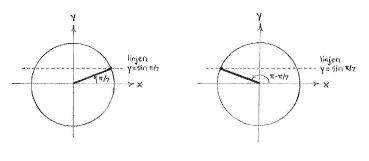
the line \displaystyle {y=\sin \pi }/{7}\; the line \displaystyle {y=\sin \pi }/{7}\;
Because of symmetry, we have that this angle is the reflection of the angle
\displaystyle {\pi }/{7}\;
in the
\displaystyle y-axis, i.e.
\displaystyle v=\pi -{\pi }/{7}\;={6\pi }/{7}\;.
