Lösung 4.2:6

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.2:6 moved to Solution 4.2:6: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
We can work out the length we are looking for by taking the difference
-
<center> [[Image:4_2_6.gif]] </center>
+
<math>a-b\text{ }</math>
-
{{NAVCONTENT_STOP}}
+
of the sides
 +
<math>a</math>
 +
and
 +
<math>b</math>
 +
in the triangles below:
 +
 
[[Image:4_2_6_13.gif|center]]
[[Image:4_2_6_13.gif|center]]
[[Image:4_2_6_2.gif|center]]
[[Image:4_2_6_2.gif|center]]
 +
 +
If we take the tangent of the given angle in each triangle, we easily obtain
 +
<math>a</math>
 +
and
 +
<math>b</math>:
 +
 +
[[Image:4_2_6_13.gif|center]]
[[Image:4_2_6_13.gif|center]]
[[Image:4_2_6_4.gif|center]]
[[Image:4_2_6_4.gif|center]]
 +
 +
<math>a=1\centerdot \tan 60^{\circ }=\frac{\sin 60^{\circ }}{\cos 60^{\circ }}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}</math>

Version vom 08:29, 29. Sep. 2008

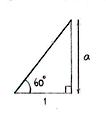
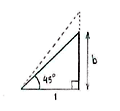
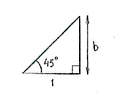
We can work out the length we are looking for by taking the difference \displaystyle a-b\text{ } of the sides \displaystyle a and \displaystyle b in the triangles below:

If we take the tangent of the given angle in each triangle, we easily obtain \displaystyle a and \displaystyle b:


\displaystyle a=1\centerdot \tan 60^{\circ }=\frac{\sin 60^{\circ }}{\cos 60^{\circ }}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:6“