Lösung 4.2:5a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.2:5a moved to Solution 4.2:5a: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Because
-
<center> [[Image:4_2_5a.gif]] </center>
+
<math>\text{135}^{\circ }\text{ }=\text{ 9}0^{\circ }\text{ }+\text{45}^{\circ }</math>,
-
{{NAVCONTENT_STOP}}
+
<math>\text{135}^{\circ }\text{ }</math>
 +
is an angle in the second quadrant which makes an angle of
 +
<math>\text{45}^{\circ }</math>
 +
with the positive
 +
<math>y</math>
 +
-axis.
 +
 
 +
 
[[Image:4_2_5_a1.gif|center]]
[[Image:4_2_5_a1.gif|center]]
 +
 +
We can determine the point on the unit circle which corresponds to
 +
<math>\text{135}^{\circ }\text{ }</math>
 +
by introducing an auxiliary triangle and calculating its edges using trigonometry.
 +
 +
[[Image:4_2_5_a2.gif|center]]
[[Image:4_2_5_a2.gif|center]]
 +
 +
opposite<math>=1\centerdot \sin \centerdot 45^{\circ }=\frac{1}{\sqrt{2}}</math>
 +
 +
adjacent
 +
<math>=1\centerdot \cos \centerdot 45^{\circ }=\frac{1}{\sqrt{2}}</math>
 +
 +
 +
The coordinates of the point are
 +
<math>\left( -\frac{1}{\sqrt{2}} \right.,\left. \frac{1}{\sqrt{2}} \right)</math>
 +
and this shows that
 +
<math>\text{cos135}^{\circ }=-\frac{1}{\sqrt{2}}</math>.

Version vom 07:56, 29. Sep. 2008

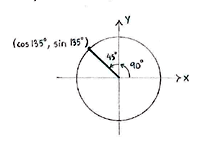
Because \displaystyle \text{135}^{\circ }\text{ }=\text{ 9}0^{\circ }\text{ }+\text{45}^{\circ }, \displaystyle \text{135}^{\circ }\text{ } is an angle in the second quadrant which makes an angle of \displaystyle \text{45}^{\circ } with the positive \displaystyle y -axis.


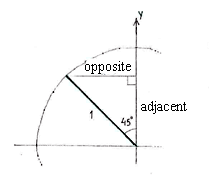
We can determine the point on the unit circle which corresponds to \displaystyle \text{135}^{\circ }\text{ } by introducing an auxiliary triangle and calculating its edges using trigonometry.


opposite\displaystyle =1\centerdot \sin \centerdot 45^{\circ }=\frac{1}{\sqrt{2}}

adjacent \displaystyle =1\centerdot \cos \centerdot 45^{\circ }=\frac{1}{\sqrt{2}}


The coordinates of the point are \displaystyle \left( -\frac{1}{\sqrt{2}} \right.,\left. \frac{1}{\sqrt{2}} \right) and this shows that \displaystyle \text{cos135}^{\circ }=-\frac{1}{\sqrt{2}}.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:5a“