Lösung 4.2:2f
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (Lösning 4.2:2f moved to Solution 4.2:2f: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | {{NAVCONTENT_START}} | ||
| - | <center> [[Image:4_2_2f.gif]] </center> | ||
| - | {{NAVCONTENT_STOP}} | ||
[[Image:4_2_2_f.gif|center]] | [[Image:4_2_2_f.gif|center]] | ||
| + | |||
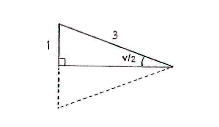
| + | Because the triangle is isosceles (two sides have the same length), it can be divided up into two right-angled triangles of the same size by introducing a side which divides the angle | ||
| + | <math>v</math> | ||
| + | in half. | ||
| + | |||
| + | If we look at one of the triangles, we can set up the trigonometrical relation | ||
| + | |||
| + | |||
| + | <math>\text{sin }\frac{v}{2}=\frac{1}{3}</math>, | ||
| + | |||
| + | which is an equation for | ||
| + | <math>v</math>. | ||
Version vom 11:38, 28. Sep. 2008
Because the triangle is isosceles (two sides have the same length), it can be divided up into two right-angled triangles of the same size by introducing a side which divides the angle \displaystyle v in half.
If we look at one of the triangles, we can set up the trigonometrical relation
\displaystyle \text{sin }\frac{v}{2}=\frac{1}{3},
which is an equation for \displaystyle v.