Aus Online Mathematik Brückenkurs 1

Version vom 09:37, 9. Sep. 2008 (bearbeiten) Tekbot (Diskussion | Beiträge) K (Lösning 4.1:7a moved to Solution 4.1:7a: Robot: moved page) ← Zum vorherigen Versionsunterschied		Version vom 11:52, 27. Sep. 2008 (bearbeiten) (rückgängig) Ian (Diskussion | Beiträge) Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
-	{{NAVCONTENT_START}}	+	As the equation stands, it is difficult directly to know anything about the circle, but if we complete the square and combine
-	<center> [[Image:4_1_7a-1(2).gif]] </center>	+	<math>x</math>
-	{{NAVCONTENT_STOP}}	+	- and
		+	<math>y</math>
		+	- terms together in their own respective square terms, then we will have the equation in the standard form,
		+
		+
		+	<math>\left( x-a \right)^{2}+\left( y-b \right)^{2}=r^{2}</math>
		+
		+
		+	and we will then be able to read off the circle's centre and radius.
		+
		+	If we take the
		+	<math>x</math>
		+	- and
		+	<math>y</math>
		+	- terms on the left-hand side and complete the square, we get
		+
		+
		+	<math>x^{2}+2x=\left( x+1 \right)^{2}-1^{2}</math>
		+
		+
		+	<math>y^{2}-2y=\left( y-1 \right)^{2}-1^{2}</math>
		+
		+	and then the whole equation can be written as
		+
		+
		+	<math>\left( x+1 \right)^{2}-1^{2}+\left( y-1 \right)^{2}-1^{2}=1</math>
		+
		+
		+	or, with the constants moved to the right-hand side,
		+
		+
		+	<math>\left( x+1 \right)^{2}+\left( y-1 \right)^{2}=3</math>
		+
		+
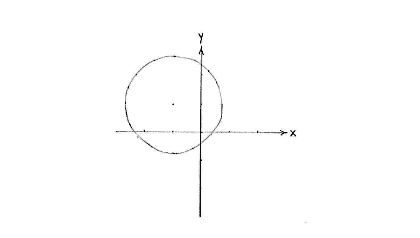
		+	This is a circle having its centre at
		+	<math>\left( -1 \right.,\left. 1 \right)</math>
		+	and radius
		+	<math>\sqrt{3}</math>.
		+
	{{NAVCONTENT_START}}		{{NAVCONTENT_START}}
	<center> [[Image:4_1_7a-2(2).gif]] </center>		<center> [[Image:4_1_7a-2(2).gif]] </center>
	{{NAVCONTENT_STOP}}		{{NAVCONTENT_STOP}}

---

Version vom 11:52, 27. Sep. 2008

As the equation stands, it is difficult directly to know anything about the circle, but if we complete the square and combine \displaystyle x - and \displaystyle y - terms together in their own respective square terms, then we will have the equation in the standard form,

\displaystyle \left( x-a \right)^{2}+\left( y-b \right)^{2}=r^{2}

and we will then be able to read off the circle's centre and radius.

If we take the \displaystyle x - and \displaystyle y - terms on the left-hand side and complete the square, we get

\displaystyle x^{2}+2x=\left( x+1 \right)^{2}-1^{2}

\displaystyle y^{2}-2y=\left( y-1 \right)^{2}-1^{2}

and then the whole equation can be written as

\displaystyle \left( x+1 \right)^{2}-1^{2}+\left( y-1 \right)^{2}-1^{2}=1

or, with the constants moved to the right-hand side,

\displaystyle \left( x+1 \right)^{2}+\left( y-1 \right)^{2}=3

This is a circle having its centre at \displaystyle \left( -1 \right.,\left. 1 \right) and radius \displaystyle \sqrt{3}.